Análisis de circuitos 2.
Las aproximaciones son necesarias para el cálculo de circuitos. En electrónica es muy necesario el uso de aproximaciones. Así, no es lo mismo decir que tengo 20 años, que 20 años y 2 meses, y si queremos una tercera aproximación diremos que tenemos 20 años, 2 meses, 12 días, 18 horas, 15 minutos y 37 segundos. Esta última es una aproximación real, pues es la más precisa de todas. La primera aproximación es la más básica, pero es real, pero se excluyen detalles; y la 2ª aproximación es básica pero tiene algún detalle más que en la primera aproximación. En electrónica y electricidad utilizaremos inicialmente una primera y segunda aproximación, ya que una aproximación ideal sería incluir detalles que ralentizarían la resolución del problema, pero habrá situaciones en la que te pidan una aproximación real.
Fuentes de tensión.
Una fuente ideal de tensión es aquella que produce una salida en la carga de tensión constante. En una primera aproximación y, por poner un ejemplo, una batería que tuviese una resistencia interna nula, haría que en la carga la tensión fuese constante. Así, una salida en la carga de una resistencia variable de 1Ω a 1MΩ, producirá una salida de tensión constante con una fuente de 10 voltios, 10 voltios exactos en R1.
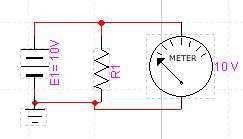
En una segunda aproximación, acercándonos mas a la realidad, incluimos la resistencia interna de la fuente que modifica la tensión de salida.
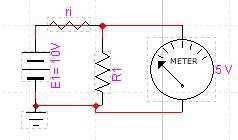
Al incluir en el cálculo la resistencia interna, la salida en la carga cambia a 5 voltios cuando la carga tiene un valor de 1Ω. Esto se debe a que la intensidad de la batería se divide en 2 resistencias de igual valor por lo que la tensión total se divide en las 2 resistencias. Según aumente el valor de la carga, aumentará la caída de tensión en ella, pero por muy grande que esta sea, jamás alcanzará los 10 voltios de la fuente de tensión. Por lo tanto, sabemos que la resistencia interna modifica la salida de alimentación en la carga, pero cuando la carga es un tanto superior a la resistencia interna apenas modifica la tensión en la carga. Pues por lo tanto podemos definir una norma a partir de este momento y es que la resistencia interna de una fuente se puede despreciar cuando la resistencia de carga del circuito sea 100 veces superior a la resistencia interna. Por lo tanto una fuente de tensión constante es:
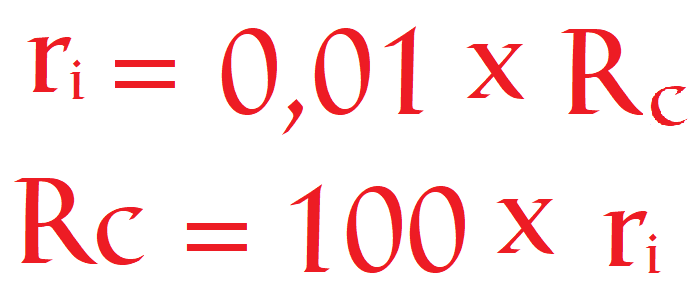
La definición de fuente de tensión constante se aplica tanto a las fuentes de continua como de alterna. Imagina que una fuente alterna tiene una resistencia interna de 50Ω. ¿Para qué resistencia de carga es constante la fuente?
Para calcular la fuente constante calculamos la resistencia de carga mínima. Para ello multiplicamos el valor de “ri” por 100 y el resultado es de 5KΩ. Mientras que la carga sea mayor o menor de 5KΩ, la tensión de la fuente es constante y podemos ignorar la “ri” de la fuente.
Fuentes de corriente.
Una fuente de tensión mantiene la tensión constante en la carga. Una fuente de corriente continua es distinta; produce una corriente por la carga constante para diferentes resistencias de carga. Un ejemplo de fuente de corriente constante es, por ejemplo, una batería con una resistencia interna elevada.
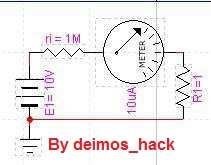
En este caso la corriente de la carga vale:
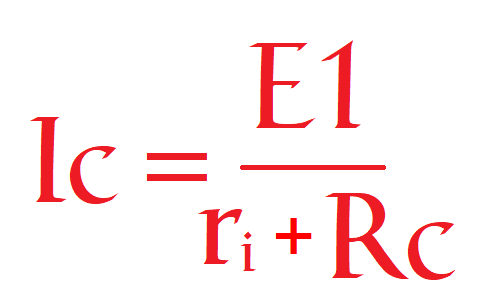
Por lo que, y según muestra el amperímetro tiene una intensidad por ella de 10µ amperios. En estos cálculos las resistencias de cargas pequeñas no tienen efecto sobre la intensidad de salida, pero según se aumente el valor de Rc, llegará un momento en que si modificará la intensidad. Por, al igual que anteriormente, establecemos que para que la fuente de corriente sea constante, la resistencia de carga tendrá que ser 100 veces inferior a la resistencia de carga. Es decir una fuente de corriente constante es:
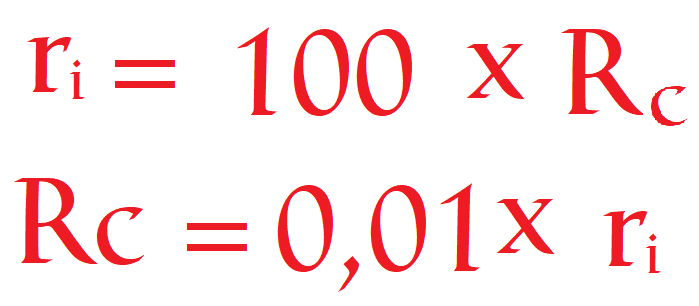
La fuente de corriente de 2mA tiene una resistencia interna de 5MΩ. Para que la fuente de corriente sea constante, ¿cuál es el rango aceptable para la Rc?
La solución es fácil. Multiplica 0,01 * ri = 5000000 * 0,01 =50KΩ. Es decir que el rango de resistencia de carga en el cual la fuente de corriente es constante, va desde 0 a 50KΩ.
Teorema de Thevenin.
El teorema de Thevenin es una teoría sobre la cual se puede sustituir un circuito complejo por una única resistencia y una única fuente de alimentación. Para calcular la tensión Thevenin se define como la tensión que aparece en la carga cuando se desconecta la carga. También se llama tensión a circuito abierto.
La resistencia Thevenin es la resistencia que se obtiene cuando se mide el circuito con un óhmetro al cortocircuitar todas las fuentes de alimentación y deshacerse de la carga. Según este teorema, calcular la tensión Thevenin es sencillo, pero calcular la resistencia es un poco complicado, con lo que hay que prestar más atención. Se puede calcular que la intensidad por la carga en un circuito Thevenin es:
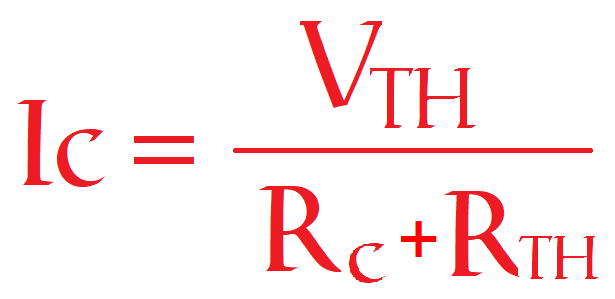
Veamos algunos ejemplos:
Calcula la tensión Thevenin y la resistencia Thevenin en este circuito:
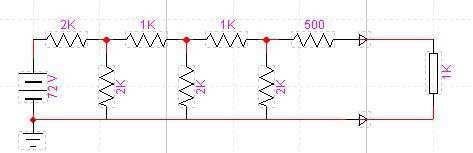
Cuando 2 resistencias están en paralelo con otras, se representará el conjunto con el símbolo “||” que significa en “en paralelo con”. Para resolver el circuito, lo más sencillo es resolverlo por diagramas:
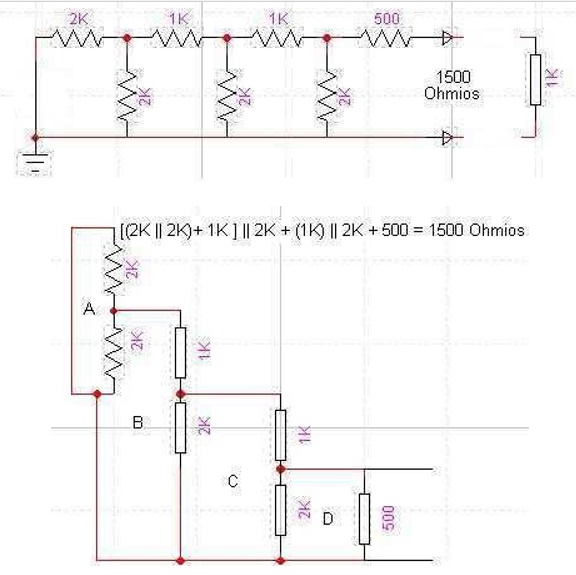
Para la resolución del sistema primero desconecta la resistencia de carga y cortocircuita la fuente de tensión para medir la resistencia que existe entre los terminales del sistema.
En cada malla, la resistencias están en paralelo y se suma su resultante con el valor de la siguiente resistencia de la malla contigua de la forma que puedes ver arriba, de tal manera que la resultante de la resistencia es la suma del conjunto.
Teorema de Norton.
La corriente de Norton IN, se define como la corriente por la carga cuando la resistencia de carga se cortocircuita. Como te habrás dado cuenta, cuando se cortocircuita un circuito, la corriente tiende a infinito, por lo que el circuito, tiende a quemarse debido a la gran intensidad. Por esta observación la corriente de Norton se denomina corriente por la carga en cortocircuito.
La resistencia de Norton es la resistencia que un óhmetro mide en los terminales de carga cuando la resistencia de carga está desconectada. Si te has dado cuenta:
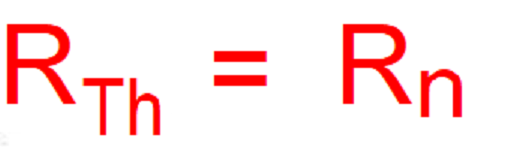
Norton probó que cualquier circuito complicado producirá la misma tensión en la carga que un circuito simple con una fuente de corriente y una resistencia Norton. El teorema de Norton se expresa así:
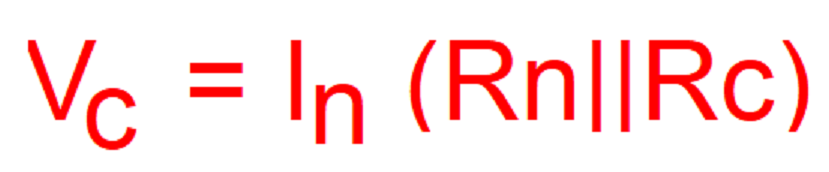
Siendo Vc, la tensión en la carga; In, la intensidad Norton; Rn la resistencia Norton; y Rc la carga del circuito.
En este momento hay que decir que el circuito Thevenin está formado por una tensión Thevenin en serie con una resistencia Thevenin; y después la carga; en un circuito Norton, hay una fuente de corriente en paralelo con la resistencia Norton, y después la carga; como se muestra a continuación:
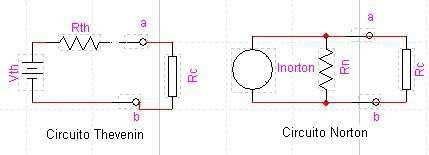
Relación entre teoremas.
Las resistencias Thevenin y Norton son de igual valor, pero de diferente localización. La resistencia Thevenin está en serie con la fuente y la resistencia Norton está en paralelo con la fuente de corriente. La relación que une ambos teoremas es la siguiente:
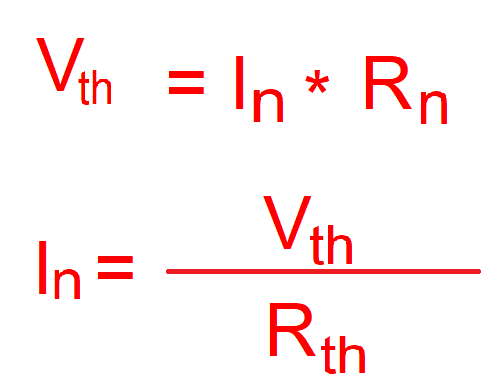
Por lo que conociendo 2 términos podemos calcular todos los términos.
Ecuaciones de Kenelly.
Las ecuaciones de Kenelly son unas operaciones matemáticas que permiten transformar una red resistiva en forma de malla a otra red eléctrica en forma de estrella y viceversa. El proceso para la transformación se describe a continuación:
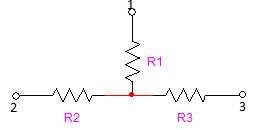
Tenemos un circuito en forma de estrella:
Y queremos cambiarla por un circuito en triángulo como el siguiente:
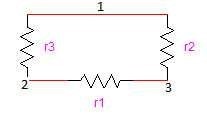
Para esta transformación, primero se numeran los vértices de las configuraciones, tal como se ve en la imagen superior. Las resistencias de la estrella se diferencian de las otras por el nombre en mayúsculas o minúsculas según sea estrella a triángulo (se usan las mayúsculas para la estrella y las minúsculas para el triangulo). Para sacar las formulas que utilizaremos más tarde, vamos a igualar los valores de las resistencias de ambas configuraciones, de la forma que R1 = r1, etc., etc.:
De esta forma, y midiendo las resistencias entre los terminales 1 y 2, 1 y 3, 2 y 3, obtenemos las ecuaciones generales:
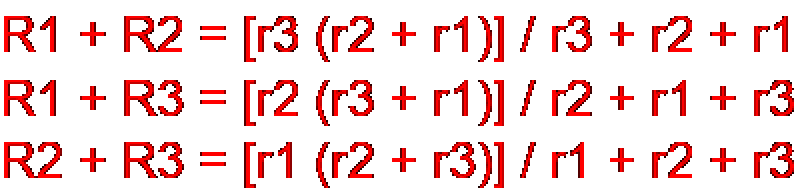
Y teniendo estas operaciones, podemos determinar los valores de las configuraciones estrella - triángulo y viceversa.

Estas formulas nos hacen un gran favor cuando tenemos que resolver circuitos complejos con varias mallas en los que no podemos calcular mediante ningún otro método como Ohm o el método de las mallas, por citar alguno.
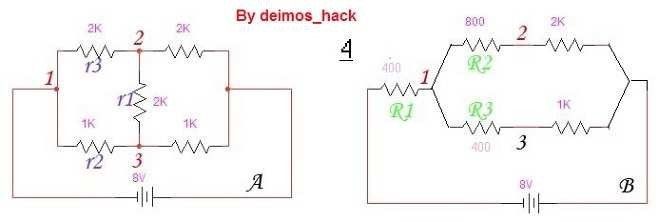
En el circuito A, te muestro el circuito en forma de triángulo que queremos transformar en estrella (B). Como puedes ver, lo primero que he hecho es asignar los puntos al triángulo A empezando por la izquierda y en sentido de las agujas del reloj (que es el mismo sentido que se cogía si recuerdas al realizar los cálculos por el método de las mallas).
Aunque al circuito hay que asignarle un poco de imaginación (circuito A), el triángulo está designado por las resistencia r3, r1 y r2; siendo r1 la base del triángulo y r3, r2 los lados del triángulo que se unen por el punto 1.
Para obtener el circuito equivalente de estrella (circuito B), utilizamos las ecuaciones de Kennelly de transformación a estrella, que sustituyendo los valores nos dan:
R1 = [1KΩ x 2KΩ] ÷ 2KΩ + 2KΩ + 1KΩ = 400Ω
R2 = [2KΩ x 2KΩ] ÷ 2kΩ + 2KΩ + 1KΩ = 800Ω
R3 = [1KΩ x 2KΩ] ÷ 2KΩ + 2KΩ + 1KΩ = 400Ω
Valores que aplicamos y construimos el circuito B según se muestra, con los puntos de la estrella también en sentido de las agujas del reloj.
Si eres buen observador, te abrás dado cuenta de que la configuración del triángulo y la estrella no son la misma (aunque eso es obvio, no me refiero a su estructura física), si no a la forma de asignar las resistencia a cada lugar que le corresponda.
En el circuito A, la resistencia r2 y r3 están unidas mediante el punto 1 por un extremo y por el otro a la resistencia r1, por lo que las resistencia r2 y r3 forman lo que se conoce como los lados del triángulo y r1 la base del mismo. Pero cuando conectes r2 y r3 no lo puedes conectar de forma altruista, ya que como ves, en el punto 2 del triángulo, está conectado r3 y en punto 3, la resistencia r2.
Cuando ya has hecho la transformación en estrella, la estrella si se configura de la forma correcta según vaya insertando los puntos de control se agregan las resistencias transformadas, de tal forma que cuando al inicio del circuito B en el punto 1 está la resistencia R1, en el punto 2, R2 y en el 3, R3; todas estas resistencias de estrella siguiendo las agujas del reloj en el circuito (B).
Una vez configurado y obtenido las resistencias de la estrella, solo queda resolverlo mediante Ohm. Como ves, hemos reducido un circuito de 2 mallas a 1 sola de facil resolución mediante Ohm. ¿Te dás cuenta de lo práctico que resulta Kennelly para resolver circuitos complejos? Aunque si te digo la verdad, donde esté un Tester, que te resuelva el trabajo, es mucho mejor... pero es bueno que sepas calcular circuitos por tu cuenta.
Vamos a terminar de resolver el circuito:
En el circuito B, para resolverlo, tenemos que, primero seguir unos pasos lógicos como son:
●Calcular primero la resistencia total del circuito.
●Calcular la intensidad parcial de cada rama.
●Calcular la c.d.t en el circuito.
Las cuatro resistencias que están en serie - paralelo dan un valor de:
[(800Ω + 2KΩ) x (400 + 1KΩ) ] ÷ [(800Ω + 2KΩ) + (400Ω + 1KΩ)]
Rparalelo - serie = 933,33333Ω
ahora le sumamos el valor de R1 al paralelo y obtenemos la resistencia total del circuito B.
933,33333Ω + 400Ω = 1333,33333Ω.
Que es la resistencia Thevenin. Ahora con estos datos, y sabiendo que la tensión de alimentación es de 8 voltios, nos queda que:
I = 8V ÷ 1333,33333Ω = 6 mA.
Que es la intensidad Norton.
Potencia eléctrica.
Se dice potencia al trabajo realizado para desplazar las cargas eléctricas de punto a otro del circuito. El trabajo es una unidad física y se mide en Julios (1 julio = 1N x 1m) Se utiliza la unidad del julio para medir energía, calor o trabajo. En este caso, medimos el trabajo eléctrico, y en el caso, medimos por lo que tendremos que obtener el equivalente del julio para la energía eléctrica, que en este caso se medirá en vatios/segundos. 1 julio equivale a 1 vatio por segundo.
Así de la forma que si el trabajo (julios) es igual a la energía eléctrica por el número de carga en unidad de tiempo (culombios), nos queda que:
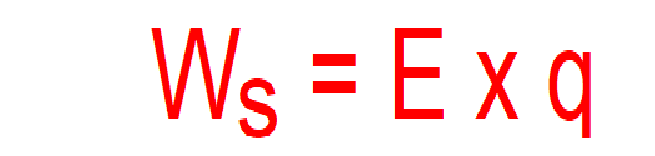
Y como la potencia es trabajo:
P = [E (voltios) x q (culombios)] ÷ segundos = julios ÷ segundos = vatios.
Ahora bien, como un culombio es un amperio por segundo, sustituyo “q” por amperios ÷ segundos y nos da la fórmula definitiva de la potencia:
P = [E x (A ÷ s)] ÷ s = E x (As ÷ s) = E x A = vatios.
Esta es la potencia que se obtiene al realizar el múltiplo de la tensión aplicada del circuito o elemento y la intensidad que circula por el mismo. Pero la potencia también se puede calcular en función de otros elementos como puede ser la resistencia.
En la resistencia, la potencia que se genera en su interior es en forma de calor debido a la oposición al paso de la corriente que ofrece dicho elemento, por lo que lo que se mide es la potencia disipada en vatios en dicho elemento o en dicho circuito (si se mide la resistencia total). Para calcular las formulas de la potencia, pensando en el circuito y ley de Ohm nos queda que:
P = V x I = [I x R] x I = I2 x R = vatios
P = V x I = V x [V ÷ R] = V2 ÷ R = vatios
Estas son las formulas para calcular los circuitos de la potencia según la resistencia. En el primer cálculo, he sustituido la tensión por su equivalente Ohm; en la segunda formula he sustituido la intensidad. El vatio suele utilizar múltiplos y submúltiplos para expresarse al igual que los demás valores eléctricos (mili, Kilo, Mega).
Otro concepto interesante es el concepto de kilovatio ÷ hora (Kwh). Esto se refiere al tiempo que tarda en consumirse una cantidad de potencia especificada. La unidad de potencia por unidad de tiempo da por resultado la formula de la energía. La unidad vatio por segundo es la fundamental. 1 kilovatio ÷ 1 hora es la potencia consumida en 3600 segundos. Esta medida se suele utilizar para el control de consumo eléctrico en una red eléctrica.

