Como ya he dicho en la teoría, es hora de poner las cosas complicadas y forzar un poco tu materia gris. Hasta ahora en el curso de electrónica para newbies has visto circuitos básicos y sencillos de resolver. Pero en la resolución de circuitos y reparación de fallas en tus placas electrónicas, no te vas a encontrar circuitos simples, sino más bien lo contrario. Por eso creo que, lo mejor para tu formación es que te esmeres un poco y que se te caliente la materia gris que tienes entre las orejas para poder prepararte para este curso que estás estudiándo y tu vida laboral.
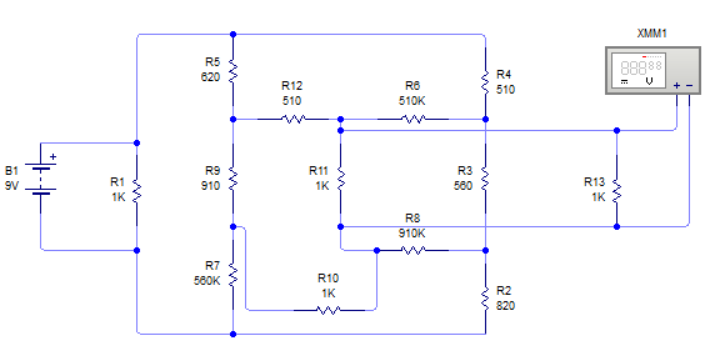
El valor de las resistencias las puedes ver en la imagen (recuerda el código de color de las resistencias) Pero te mostraré la lista de las resistencias. Como ayuda te puedo decir que necesitarás usar las transformaciones de Kenelly para poder reducir el circuito a una forma básica.
Te dejo que resuelvas tu el circuito. Si quieres ver la solución del sistema pulsa sobre el siguiente botón.
Utilizar Kenelly es una solución a la hora de transformar circuitos deltas en estrella y viceversa. Pero realmente este tipo de circuitos riguen más la lógica visual que las reglas de transformación porque son circuitos muy complejos en cuanto al número de nodos que tienen y sistemas en paralelo.

Has de tener en cuenta donde se conecta la fuente de alimentación. En nuestro ejemplo se conecta al primer cubo a través de la resistencia R1. Pero también alimenta a la resistencia R5. Con eso, estamos alimentando dos partes del cubo: la formada por la malla R4, R3 y R2. Y la malla conectada por R5, R9 y R7, cerrándose el nodo en R1 de nuevo.
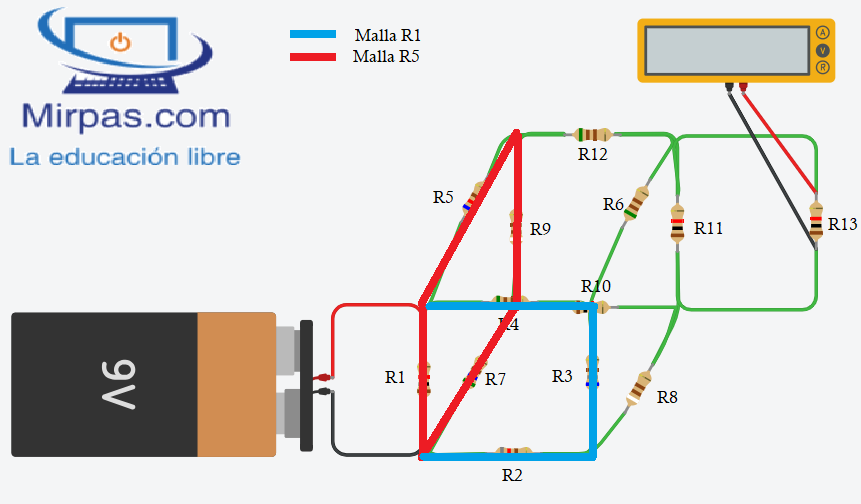
El contorno del cubo formado por R12, R11, R8 y R2 está alimentado por las resistencias R9 y R7.
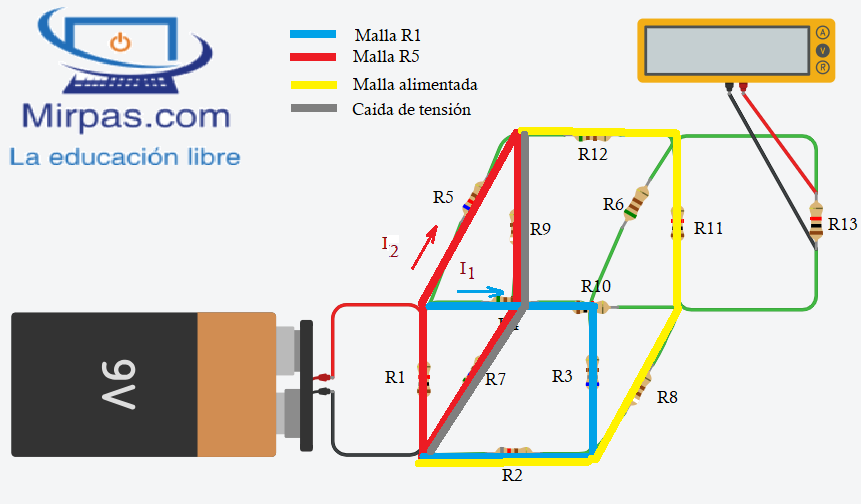
Por lo que si en la red formada por R9, y R7, caen X voltios menos ER5, y sobre la resistencia R11 se conecta la carga, ya puedes realizar un cálculo mediante Ohm.
ESTA es la solución
La tensión de la batería se aplica a R1, la cual tiene dos caras del cubo en paralelo. Por la parte de R4, R3 y R2, circula una corriente I1. Por la parte de R5, R9 y R7 circula una corriente I2. Como estas resistencias están en serie, podemos calcular la intensidad que circula por el ramal de la forma siguiente:
I2 = E ÷ R5 + R9 + R7Esto nos da una intensidad de 4,306mA. Obtenemos las caidas de tensión en las resistencias de dicha malla:
● E5 = 2,67V
● E9 = 3,91V
● E7 = 2,41V
 |
| |
|
Puedes ver que el cálculo es muy real al calculado, salvo pequeñas perdidas por fugas.
Puedes calcular por el mismo método la intensidad por la primera malla. La I1 tendrá un valor de 4,762mA. Eso nos deja unos valores de caidas:
● E4 =2,42
● E3 = 2,66V
● E2 = 3,90V
 |
| |
|
Y como he mencionado anteriormente, la caida de tensión en las resistencias R9 y R7, proporcionan la tensión a la malla en la que está conectada la carga y en concreto la resistencia R11. Así que, ya solo y mediante Ohm podemos conocer la tensión aplicada a la carga mediante una simple derivación. Teniendo en cuenta que la tensión VR9 + VR7 = 3,91V + 2,41V = 6,31V
En la malla de la carga, por derivación obtengo que la resistencia total de la cara vale 3K24Ω. Eso me da una intensidad de 1,947mA. Y proporciona una caida de tensión en cada resistencia de:
● ER12 = 0,99V
● ER11 = 1,94V
● ER9 = 1,77V
● ER2 = 1,597V
Y como la tensión que está en la carga es la de la resistencia R11, la tensión que se presenta en la carga es de 1,94V.
Problema:
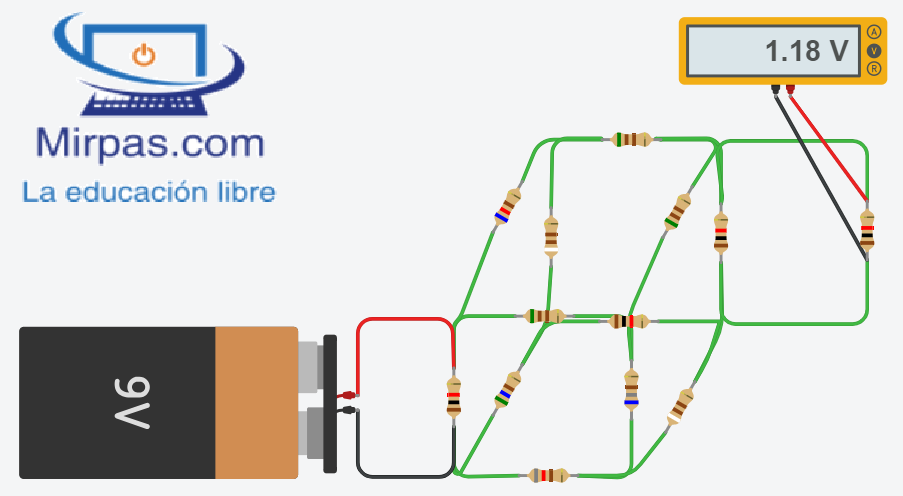
Resulta que si construyes el circuito y lo mides con un voltímetro (o incluso el propio simulador Tinkercad), podrás comprobar que la medida de la tensión no corresponde a la realidad.

Ese problema no se ha producido por un mal cálculo; simplemente no hemos tenido en cuenta las propias corrientes inversas que circulan por las redes compartidas, ya que, como en cada cara del cubo existen varias resistencias, un par de ellas se comparten con otras caras, produciéndo corrientes y tensiones que se contrarrestan.
Y es que en el cubo resistivo hemos utilizado todas las resistencias menos dos, que son la R10 y la R6. Y es precisamente esta resistencia la que, si tomas su medida, va a medir una tensión de -0,63V.

Como R6 está en paralelo con la carga, afecta a la tensión de dicha carga, por lo que a la tensión en ER11, habría que restarle esta cantidad de modo que ahora si queda la tensión medida con el tester.
Si utilizamos el simulador Tinkercad, puedes ver que la medida mostrada en el programa es muy parecida a la obtenida por los cálculos realizados.
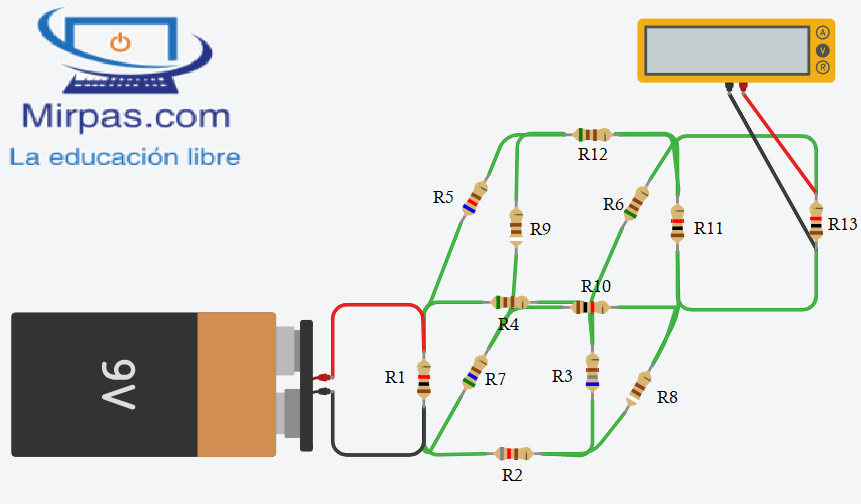
Espero que hayas tenido suerte y hayas calculado bien la respuesta. Ahora que estás inspirado, ¿podrías crear el circuito equivalente? Y para que veas que soy bueno te muestro el circuito desde otro punto de vista. Así queda el cubo resistivo cuando cambias la perspectiva:



 |
| |
|
 |
|


