Problemas resueltos.
A continuación se ofrecen una serie de ejercicios que podréis realizar vosotros mismos para comprobar cuál es el conocimiento aprendido hasta ahora en el curso de electrónica básica. Estos ejercicios propuestos, nos obligarán a repasar todos los temas propuestos hasta ahora en el modulo1 y hasta el actual tema. Por favor, esto no es un examen, sino un glosario más de estudio que te ayudará a resolver el tipo de problemas específicos y aprender cómo resolver otros problemas del mismo tipo.
Problema resuelto 1.
En el siguiente circuito, calcula la tensión, la intensidad, y la potencia por cada ramal y la tensión, intensidad y potencia total.
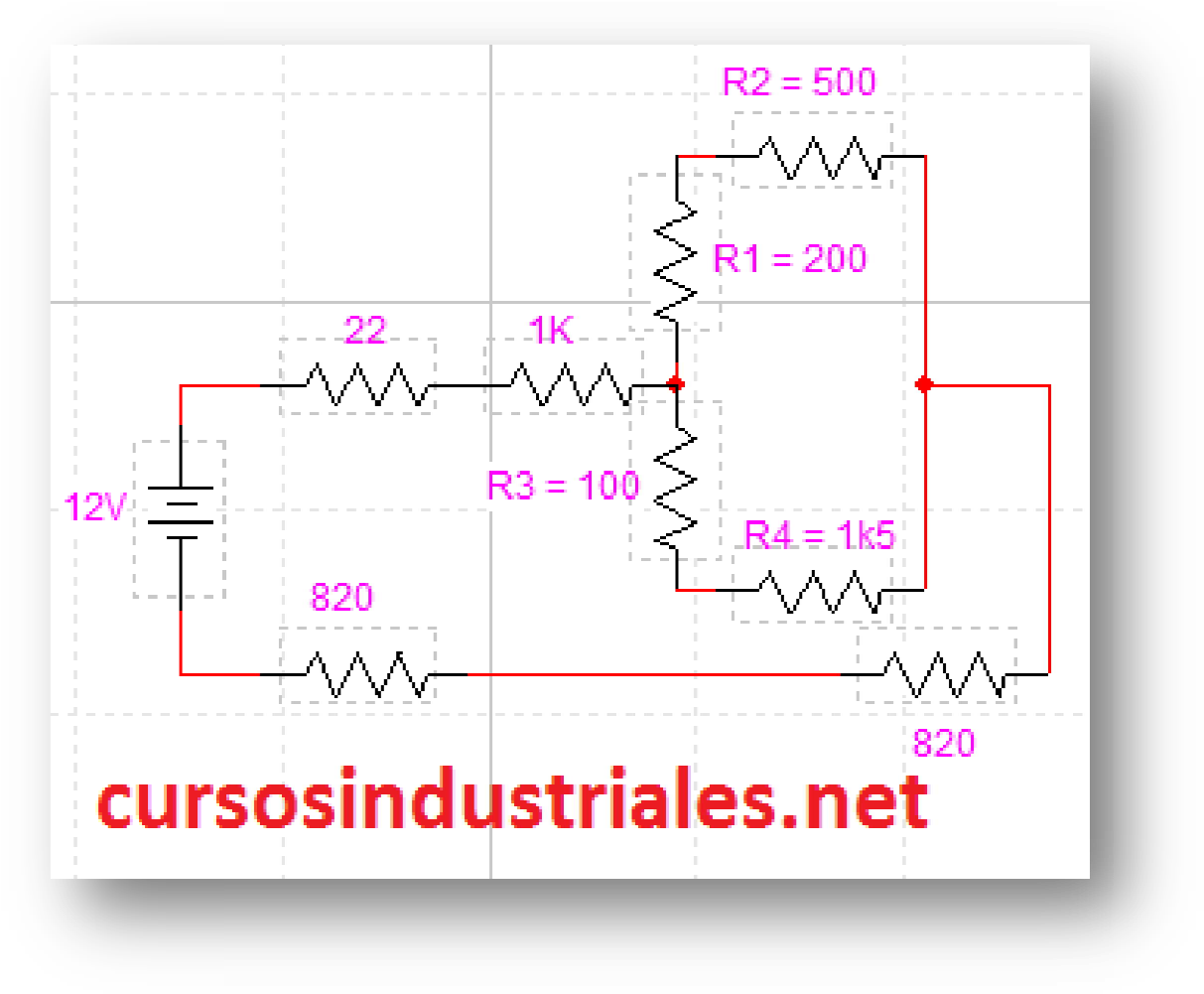
Analizando el circuito vemos que nos da un valor por defecto. El valor de la fuente de alimentación de 12 Voltios es la tensión total del circuito. Vemos también que existen 2 ramales en el camino formado el ramal R1 – R2 y el ramal R3 – R4 los cuales la intensidad se dividirá en este punto para juntarse al final del punto de salida.
No deberíamos tener ningún tipo de problema en la resolución del circuito ya que es todo resistivo y podemos utilizar Ohm.
Siempre se procede igual en la resolución de estos ejercicios:
Primero se calcula la resistencia total, convirtiendo las redes de resistencias paralelas a una serie de resistencias en serie.
Segundo se calcula la intensidad total.
Por último se termina de calcular la intensidad por cada rama y la caída de tensión en cada resistencia.
Primero:
Juntamos las resistencias de 22Ω y 1kΩ en serie, 820Ω y 820Ω:
22Ω + 1kΩ = 1022Ω..
820Ω + 820Ω = 1640Ω
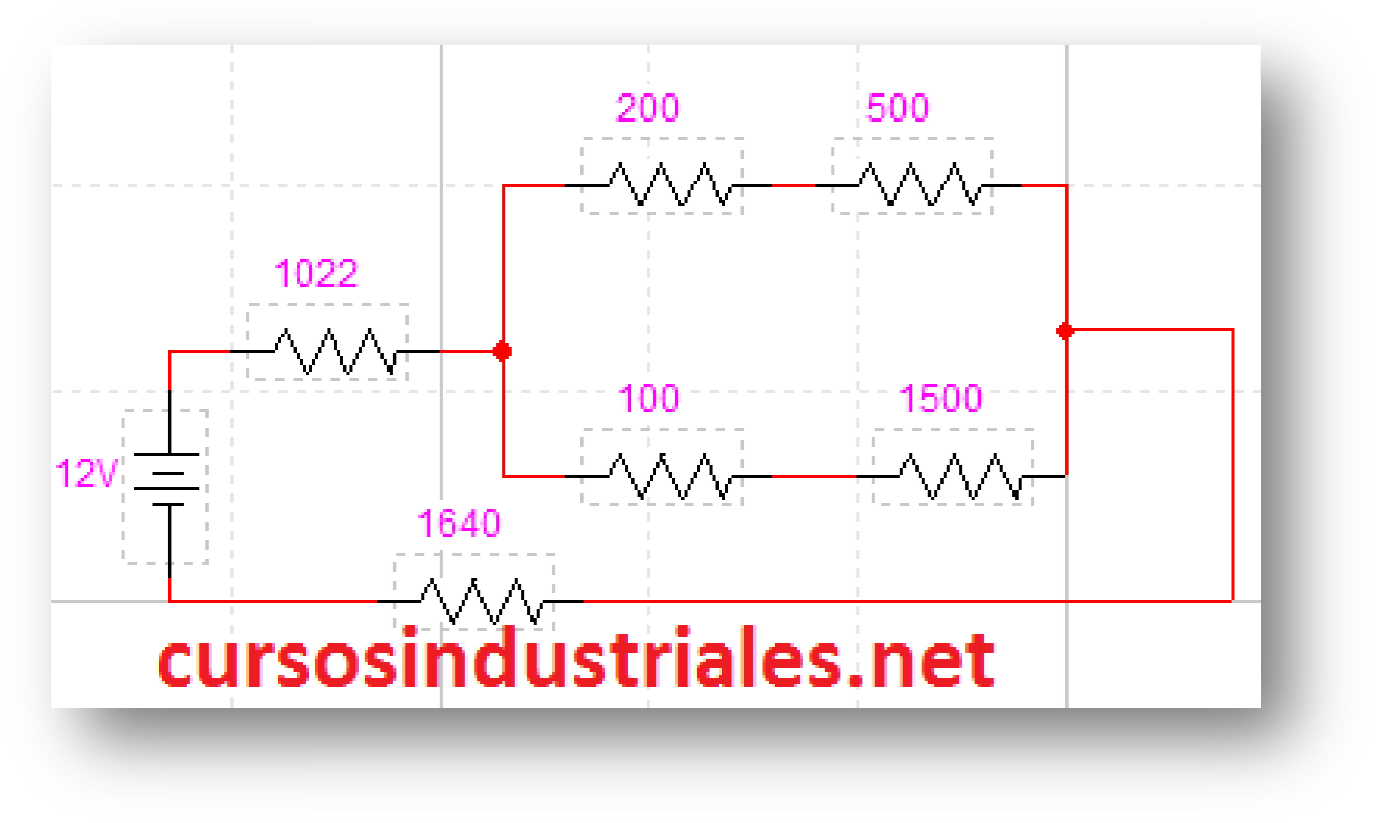
En el circuito ya he unido las resistencias en serie. Ahora queda transformar las resistencias en paralelo y sumar todas las resistencias en serie para obtener la resistencia del circuito. Para convertir la malla en paralelo a serie, se suman ambas resistencias en serie de cada rama y el resultado de cada maya se realiza la operación en paralelo para las resistencias:
200Ω + 500Ω = 700Ω.
100Ω + 1500Ω = 1k6Ω.
Ahora se obtiene el paralelo de la rama:
[ (700Ω x 1600Ω) ÷ (700Ω + 1600Ω)] = (1120000Ω ÷ 2300Ω) = 486,95Ω.
Lo que el circuito queda así:
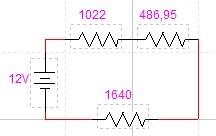
Ahora calcular la resistencia total es cosa de niños:
1022Ω + 486,95Ω + 1640Ω = 3148,95652173913Ω.
Segundo:
Teniendo los valores de E y la resistencia total, podemos calcular la intensidad total del circuito.
I = V ÷ R =
12V ÷ 3148,95652173913
I = 0,0038 A, es decir, 3,8mA.
Como último paso nos queda calcular las caídas de tensión en cada rama, la potencia total y la potencia en cada resistencia. La potencia en cada resistencia lo dejaremos para otros ejercicios. Simplemente debes aplicar la intensidad de corriente que circula por la resistencia en concreto y multiplicarla por la tensión aplicada a ella. Para calcular la caída de tensión en cada rama se procede partiendo de la misma intensidad en el circuito anterior.
En el primer grupo de resistencias, caerán:
0,0038A x 1022Ω = 3,894V.
En la rama de paralelo caerán:
0,0038A x 486,95Ω = 1,855V.
En el último grupo:
0,0038A x 1640Ω = 6,25V.
Ahora volviendo al circuito inicial, ¿sabrías calcular las caídas de tensiones en cada resistencia independiente y las intensidades por las ramas en paralelo?

La resolución se hace en base de lo que ya sabes. En el primer tramo, en las dos resistencias en serie caen 3,894V, y como la intensidad es la misma en cada una de estas dos resistencias, deducimos que:
VR22 = I x R22 = 0,0038A x 22Ω = 0,0836V.
VR1KΩ = I x R1KΩ = 0,0038A x 1000 = 3,8V
Ahora si sumamos ambas caídas de tensión de estas resistencias:
VR22Ω + VR1KΩ = 0,0836V + 3,8V = 3,894V.
Igual que el primer valor. Para las últimas resistencias en serie se procede de manera igual a la anterior:
VR820Ω = I x 820Ω =0,0038A x 820Ω = 3,116V x 2 (son dos resistencias iguales) = 6,25V.
Ahora es cuando existe algo de complicación. Calcular las caídas en las ramas en paralelo. Antes de calcular las caídas de tensión en cada rama, hay que calcular las intensidades parciales que circulan por los ramales. Para ello, sabiendo que en todo el conjunto en paralelo van a caer 1,855V procedemos de la siguiente forma:
En el primer ramal la resistencia total era de 700 ohmios. Aplicando la caída de tensión de la rama total a ese valor, nos da una intensidad de paso, y esa será la I1:
1,855V ÷ 700Ω = 0,0265A = 2,65mA.
Haciendo lo mismo con la otra rama en paralelo:
1,855V ÷ 1600Ω = 0,001160A.
Que esto será la I2 que pasa por la otra rama. Si sumamos las intensidades parciales I1 + I2 nos dará la Itotal.
0,00265A + 0,001160A = 0,00386A.
Para calcular la potencia total del circuito, procedemos a realizar la multiplicación de la tensión total por la intensidad total del mismo:
12V x 0,00386A = 0,04632W = 46,32mW
Resumiendo:
E = 12V
I = 0,00386A
R = 3149 ohmios
I1 = 0,0265A
I1 = 0,00116A
V1 = 3,90V
V2 = 1,86V
V3 = 6,24V
Ahora, ¿te animas a calcular la tensión en cada resistencia independiente?
Problema resuelto 2.
En el siguiente circuito conocemos algunos datos, pero desconocemos las demás variables. En algunas ramas están expresados los valores de tensión y en otras los valores de la intensidad por la resistencia. Calcula mediante los conocimientos que has aprendido a lo largo del curso las variables que faltan.
NOTA: Este ejercicio lo ha superado solo el 35% de los ingenieros mediante cálculos. El 65% restante lo ha deducido utilizando un aparato de medida eléctrico.
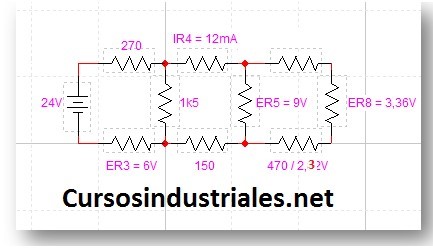
Los valores que nos han dado son la intensidad total del circuito, y la tensión Thevenin:
E = 24V
I = 20mA.
¿Cómo empezarías a desarrollarlo?
Pues el camino más simple sería coger un multímetro y medir los valores en cada componente del circuito. Pero como lo que queremos es calcularlo, no te va a servir de nada el Tester en este momento.
Analicemos el circuito:
El circuito está formado por tres mallas resistivas y una fuente de alimentación que alimenta al circuito. Cada malla está formada por 3 resistencias y una resistencia es común a la otra malla. Por norma general en estos circuitos, la resistencia que se comparte con la malla siguiente, es la resistencia de carga de esa malla.
Por tanto establecemos las resistencias de carga de la malla de la izquierda con el valor de 1k5 ohmios, la resistencia de carga de la malla central con la tensión de 9V y la carga final de la malla de la derecha.
En estos circuitos, la carga de cada malla proporciona la tensión de alimentación a la malla siguiente. Esto es así porque la carga está en paralelo con la malla siguiente, y a la vez está en serie con los elementos de su malla. Lo mejor para resolver estos circuitos es ir paso a paso y malla por malla.
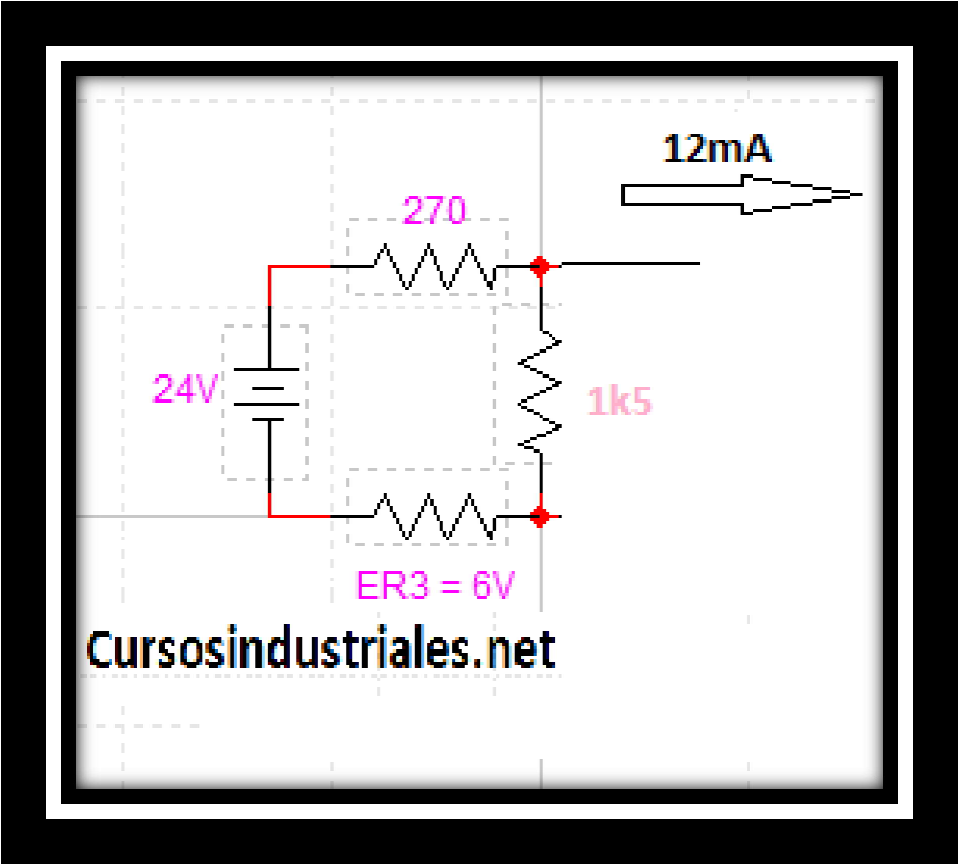
Desde este punto de vista, sabemos que R1 (270Ω) está en serie con R2 (1k5Ω) y R3 (cuya caída de tensión es de 6V). Pero R2 (1k5Ω) está en paralelo con la malla central, lo que indica que por R2 y R3 pasará otra corriente diferente a la corriente que pasará por R1.
Sabemos que la corriente que va a pasar por la malla central es de 12mA. Entonces, si por R1 va a pasar la corriente total, y por R2 y R3 otra corriente, sabiendo la corriente de la malla central, está chupado calcular la corriente de estas dos resistencias:
IT = I1 + I2 = I2 = IT – I1= I2 = 0,02 A – 0,012 A =0,008A.
Es la corriente que pasará por R2 y R3. Teniendo la corriente parcial podemos calcular la caída de tensión en R2 y el valor de la resistencia R3:
VR2 = 0,008 A x 1500Ω = 12V
R3 = 6V ÷ 0,008 A = 750 ohmios.
Por tanto la maya central estará alimentada por una tensión de 12 voltios.

La resolución de las dos mallas restantes se puede realizar mediante el método del eslabón; pero vamos a resolverlo de manera tradicional con Ohm puro y duro.
En el extremo izquierdo de la malla central tenemos una resistencia de carga cuya caída de tensión es de 12 voltios con una corriente de 8mA. En la carga del extremo derecho, solo sabemos la tensión que caerá en esta resistencia, pero no su valor ni la intensidad que pasará por ella.
Lo que sí sabemos es que por R4 pasará una intensidad de 12mA, lo que, al igual que hacíamos en el anterior punto, restamos la intensidad parcial a la intensidad total para obtener la intensidad que circulará por las demás resistencias del circuito, y en este caso es de 8mA.
Por lo tanto, sabiendo que la resistencia R6 (150Ω) pasan 8mA, dejará una caída de tensión de:
ER6 = 0,008A x 150Ω = 1,2V
Como sabemos que la resistencia de carga R5 tiene una caída de tensión de 9 voltios, y que la tensión aplicada a está malla proviene de la carga de la malla anterior, podemos calcular la caída de tensión en R4:
Emalla2 = ER4 + ER5 + ER6 =
12V = ER4 + 9V + 1,2V =
ER4 = 12V – 10,2V = 1,8V
Y sabiendo lo que cae en esta resistencia y la corriente que pasa por ella, podemos calcular el valor de la resistencia:
R4 = 1,8V ÷ 0,012A = 150Ω.
última malla
En esta última malla, desconocemos cual es la intensidad que circulará por la malla, pero ahora, podemos ver que no hay más mallas y las tres resistencias están en serie; además tenemos unos valores de tensión en la resistencia R8 y R9, lo que nos ayudará a calcular la caída de tensión en R7:

Emalla3 = ER7 + ER8 + ER9
9V = ER7 + 3,36V + 2,32V
ER7 = 9V – 5,68V
ER7 = 3,32V
Ahora teniendo las caídas de tensión en cada resistencia de la malla, podemos calcular el paso de corriente por cada una, teniendo en cuenta que la corriente pasa ahora en serie por todas las resistencias (al ser la última malla), la corriente que pase por cualquiera de ellas, es la corriente total de la malla. Pero para calcular la I tenemos que coger la intensidad de referencia general y es la que proporciona la carga de la malla central de 9V. Y como nos falta el valor de la resistencia R7 y la resistencia de carga de la última malla, se nos hace más complicado encontrar el valor adecuado:
I = E (V1 + V2 + V3) ÷ (R7 + R8 + R9) =
I = 9V ÷ (470Ω + Rc + 470Ω) =
I = 9V ÷ 940Ω + RC
Esta ecuación no nos resuelve nada. Por lo tanto, usemos la lógica:
Para calcular la Resistencia de R7 (3,32V) usaremos una regla de tres en comparación con el valor que tenemos de la resistencia R9:
“Si 2,32V equivale a 470Ω, ¿Cuánto equivale 3,32V?”
2,32V ------------- 470
3,32V ------------- R7
De ahí deducimos que:
2,32VR7 = 470Ω x 3,32V
R7 = 1560,4 ÷ 2,32
R7 = 672,59 ohmios.
Y para calcular la carga procedemos de manera similar:
“Si 3,32V equivale a 672,59, ¿Cuánto equivale 3,36V?
3,32V ------------ 672,59
3,36V ------------ RC
Deduciendo:
3,32VRc = 672,59 x 3,36V
Rc = 2260 ÷ 3,32
Rc = 680Ω.
Ahora ya calculado el valor de las resistencias podemos calcular el valor de la intensidad que pasa por la rama:
I = ETotal ÷ RTotal
I = 9V ÷ (470Ω + 672,59Ω + 680Ω)
I = 9V ÷ 1823Ω
I = 0,00493A = 4,93mA.
Hemos completado todo el circuito, y hemos calculado todos los componentes y las variables del circuito eléctrico.
Como verás es muy importante el uso de las matemáticas y tener claro el objetivo que buscar para la resolución de un problema. Si mediante la intensidad calculas las caídas de tensión en cada resistencia, observarás que va a dar lo mismo que muestra el circuito, o una pequeña diferencia debida al redondeo efectuado en el valor de la resistencia.
Espero que hayas entendido estos conceptos que en otros cursos de electrónica ampliaremos para mayor rendimiento técnico en circuitos electrónicos.
En la sección de videos podrás ver estos conceptos de manera visual.
