Circuitos eléctricos con corriente alterna.
El estudio de elementos pasivos alimentados con corriente alterna es un estudio que el alumno de electrónica tiene que aprender, ya que con ellos se da muchos de los fenómenos que más tarde rellenarán huecos culturales de los que ahora dispones. Hasta ahora hemos visto los fenómenos que ocurrían en elementos pasivos alimentados con corrientes continuas. En esta práctica veremos lo que ocurre cuando a dichos elementos se les alimentan con corrientes alternas.
Circuito CA alimentándo a una resistencia.
Ayudándonos de un montaje real, podremos observar la forma de onda en el osciloscopio de un circuito alimentado por corriente alterna y una resistencia de 1KΩ. El circuito a montar lo puedes ver en la siguiente imagen:
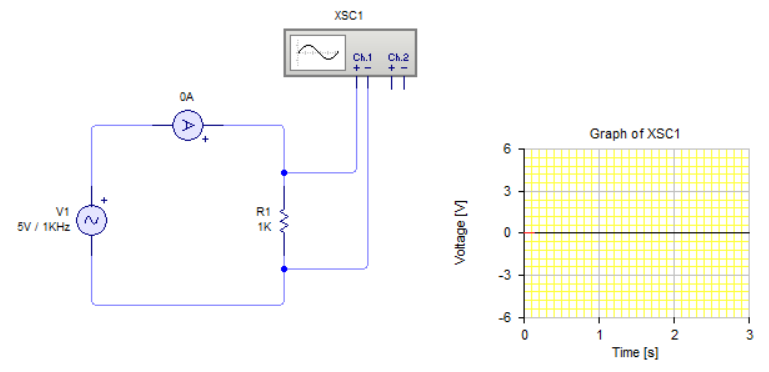
¿Sabrías decir qué corriente circula por la resistencia de carga de 1KΩ? Pues un simple vistazo al circuito implicaría que la corriente que circula por la resistencia viene dada por la ley de Ohm por lo que:
VR = R x I
Por lo que si la tensión de la fuente es de 5V y la resistencia es de 1KΩ, la intensidad de corriente será de 5x10-3A, es decir 5mA.
Pero realmente, la frecuencia afecta a la intensidad de carga, y a la tensión que se aplica a la carga.
Frecuencia y amplitud.La frecuencia y la amplitud en un sistema de alimentación están estrechamente relacionadas. Para el estudio de dicho apartado veremos el siguiente circuito.

En el circuito puedes ver un generador de señal con una frecuencia de salida de 1KHz, conectado a una resistencia de 1KΩ y cuya salida también se conecta a un osciloscopio para mostrar la forma de onda.
A dicha frecuencia, conecto en serie un amperímetro en modo alterno y obtengo que por la carga circula una intensidad de 1,62mA. Una intensidad tan baja implica que la tensión del generador sea inferior a 5V. Por lo tanto existe alguna condición que hace que la tensión del generador no sea constante a 5V pico a pico. Esa condición se llama impedancia.
Si aumento la frecuencia mediante el selector del generador de señal, lo que estoy haciendo es que los ciclos por segundo de la señal se acerquen más entre ellos. Teniéndo un offset a cero en el generador de señal, la señal no aumentará su amplitud. Es decir, a mayor frecuencia, la amplitud de la señal será la misma y por tanto la tensión tendría que ser constante. Sin embargo, aumentándo dicha frecuencia, aumenta la tensión.
En cuanto a la intensidad, ocurre un efecto contrario. A mayor frecuencia menor es la intensidad de corriente por la carga.
Así que puedes ver que la impedancia afecta también a un elemento pasivo como es la resistencia. Y no le afecta solo por el hecho de ser resistivo, sino por la propia naturaleza de la onda alterna y las características constructivas del resistor ya que presenta una inductancia residual que produce éste efecto.
La potencia disipada en la resistencia por lo tanto también varía con la frecuencia, ya que si al variar la frecuencia, aumenta o disminuye la intensidad y la tensión, aumentará y disminurá también por lo tanto, la potencia disipada en la carga.
Pm = VR x I
Como la potencia depende de la frecuencia, la potencia recibe el nombre de potencia activa.
La potencia en ca, se mide en vatios y en julios respectivamente, siendo muy empleado el termino de kilovatio-hora (kWh) para grandes cantidades de energía.
De esa manera es posible obtener la potencia media o activa a partir de los valores instantáneos de la tensión o intensidad.
Calculemos el anterior circuito.

Para el cálculo utilizaremos una primera aproximación sin tener en cuenta el efecto peculiar. Por eso, para el desarrollo del circuito tendremos que tener en cuenta la tensión de alimentación y la carga. En este caso, una fuente alterna de 5 voltios y una carga, nos indicaría que circularía una intensidad de 5V ⁄ 1KΩ = 5 x 10-3A.
En una segunda aproximación, sin tener en cuenta todavía el efecto peculiar, tendríamos que tener en cuenta la tensión eficaz del generador.
Si partimos de que la señal alterna es de 5VPP, tenemos que la tensión máxima de pico es de 2,5V. La tensión eficaz de 2,5V es:
2,5V ⁄ √2 = 1,767V.
Ahora aplicamos Ohm para saber que por la carga pasan 1,767 x 10-3A, es decir 1,7mA.
En una tercera aproximación tendríamos que tener en cuenta el efecto peculiar de la frecuencia, la constitución de la resistencia, el tipo de material, etc.
Circuito AC con condensador y resistencia.
En la siguiente imagen se muestra el circuito y formado por un condensador de 470nF y una resistencia de 1KΩ
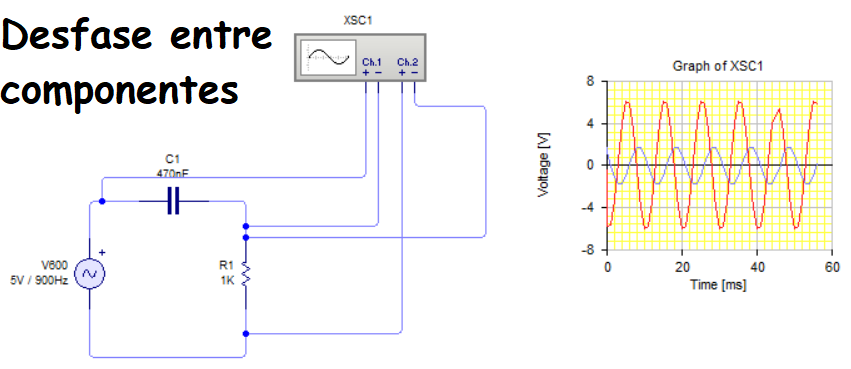
Como en el circuito no podemos visualizar la corriente (porque un osciloscopio solo muestra la tensión), utilizamos el punto medio entre ambos componentes ya que la intensidad por el circuito es la misma para ambos componentes. Así pues, en un canal tendremos la tensión resultante de la caida de tensión en la resistencia y en otro canal, la tensión en el condensador.
Puedes ver que tanto la corriente como la tensión tienen forma alterna (la caida de tensión en la resistencia es el color rojo y la intensidad del condensador el color morado). Ambas señales tienen la misma componente, pero puedes ver en el eje de las abscisas que los valores de tensión no coinciden en el tiempo. Existe un desfase de 90º entre ambas magnitudes. Concretándo, la tensión se encuentra retrasada con la intensidad.
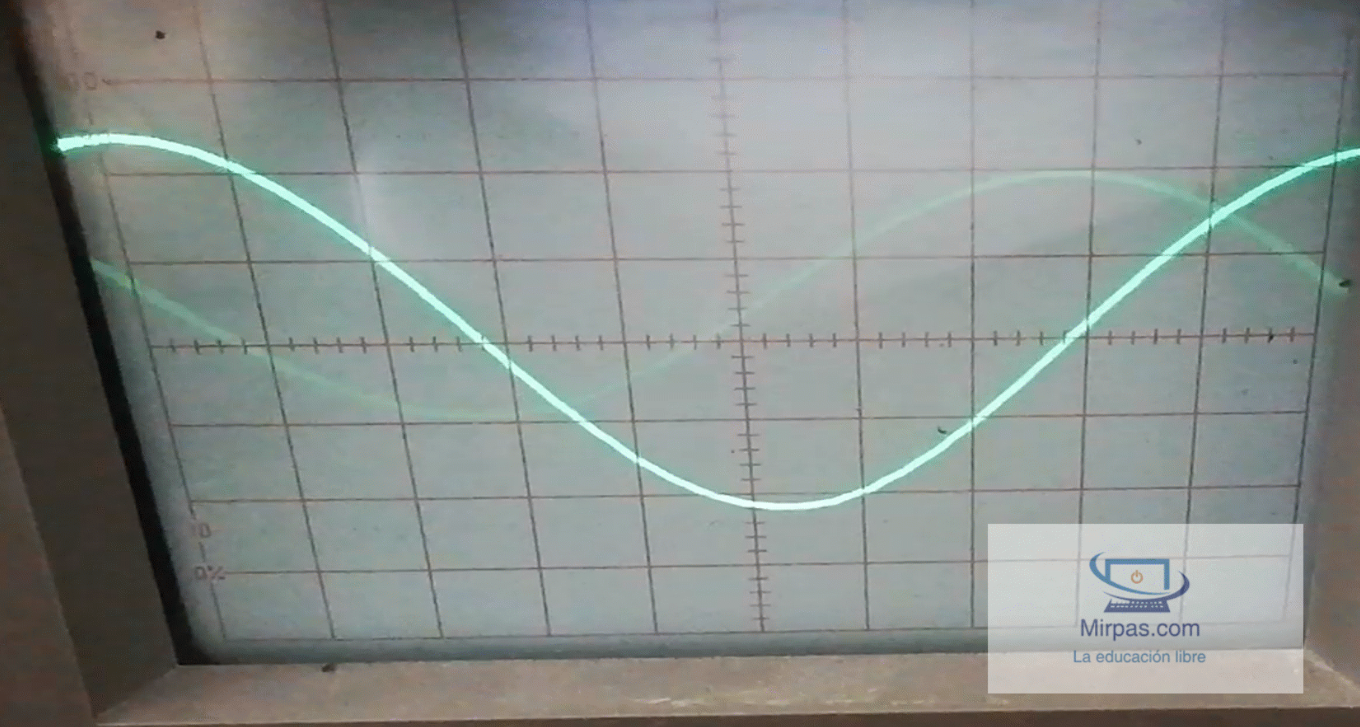
Reactancia capacitiva.Si despreciamos la resistencia y su disipación de calor, por la propia naturaleza del condensador y la corriente alterna, el condensador presenta una reactancia capacitiva que se activa con el cambio de frecuencia de acuerdo a la fórmula siguiente:
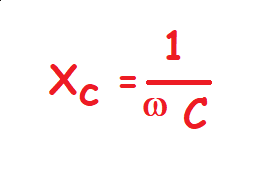
Esta fórmula viene establecida por la inversa del producto de la velocidad ángular de las pulsaciones (ω), con la capacidad del circuito. Por lo tanto, dicha reactancia disminuirá según aumente la frecuencia y aumentará mientras menor sea la frecuencia. La reactancia se expresa en ohmios cuando C, se expresa en faradios y ω en radianes por segundo. Además, cuando mayor sea la capacidad del condensador menor será la reactancia para una misma frecuencia.
Normas y leyes aplicables al circuito.En este circuito también se aplica la ley de Ohm de la forma:
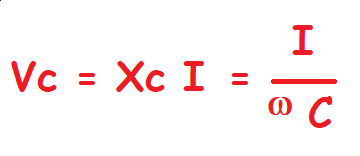
Para poder operar matemáticamente las magnitudes utilizaremos la notación compleja. Como las magnitudes se semejan a vectores, y los desfases entre las magnitudes se expresan en forma de ángulos. Así que tomándo como referencia el eje de un sistema ortogonal. Es bueno que te vayas acostumbrándo a trabajar con números complejos sobre todo en relación a circuitos en alterna.
Para representar el retraso de la tensión respecto a la corriente 90º, se utiliza:
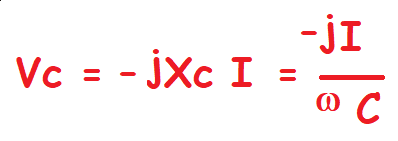
Donde j es el operacional que acompaña a la parte imaginaria de un número complejo y cuyo valor era de j = √-1.
Así la fórmula anterior compleja se puede representar como:
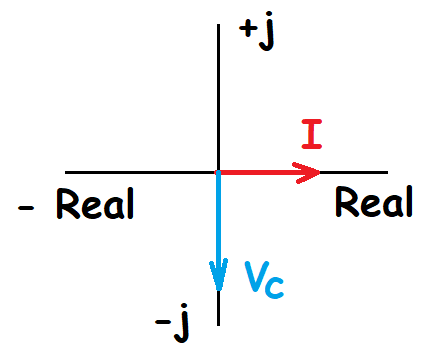
Todas las magnitudes de corriente alterna se expresarán siempre como vectores utilizándo las formas de uso: binomica, polar o trigonométrica, preferiblemente mediante las dos últimas. En cualquier caso, de la expresión se debe de obtener siempre el módulo y el argumento (valor y ángulo polar).
Por último, la potencia disipada por el condensador es nula, ya que la corriente que circula por él, se devuelve al circuito y el único consumo de energía es la de la propia resistencia. Para cálcular la potencia habría que tomar mediciones instantáneas de tensión y corriente. De ahí surgue un nuevo concepto de potencia reactiva cuyo valor es:
Pr = VC x IDonde Vc e I son los valores eficaces de los módulos de la tensión en el condensador y la corriente por el circuito. La potencia reactiva se mide en voltios-amperios reactivos.
Circuito AC con inductancia y resistencia.
Si sustituimos el condensador por una bobina, obtenemos el circuito siguiente:
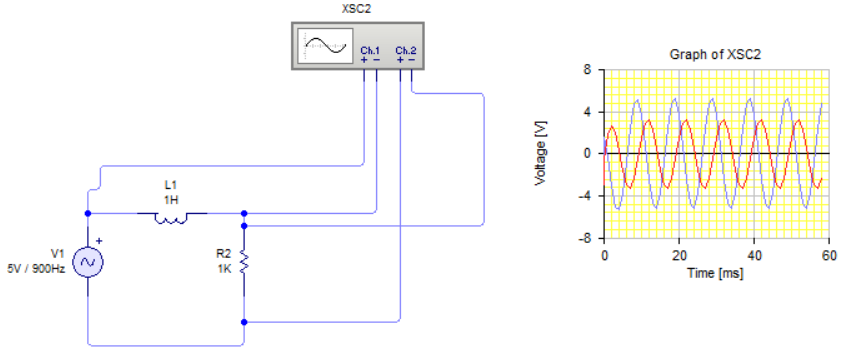
Al igual que en el anterior circuito, se produce un desfase de 90º. En este caso la corriente se retrasa respecto a la tensión. El desfase se mantiene inalterable mientras que el generador y la auoinducción estén conectados.
Reactancia inductiva.La inductáncia tiene una autoinducción ligada al paso de la corriente. Pero como la corriente es variable, la autoinducción será continua en una inductancia alimentada en ca. Por ese motivo, la inductancia presenta una resistencia física a la corriente alterna que se llama reactáncia inductiva. El valor de la reactancia inductiva depende exclusivamente del coeficiente de autoinducción de la bobina.
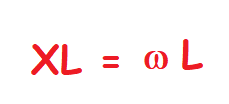
Donde ω es la pulsación de la corriente alterna. La inductancia se obtiene en ohmios cuando L se expresa en henrios y ω en rad⁄s, y como se puede observar, es directamente proporcional al coeficiente de autoinducción, por lo que mientras mayor sea éste, mayor será la reactancia inductiva. También mayor valor de las pulsaciones (frecuencia), mayor será la reactancia inductiva.
Así que la caida de tensión en la inductancia viene dada por la tensión en la bobina y la corriente del circuito de la forma que:
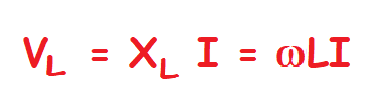
Y como existe un desfase se indica de la siguiente manera:
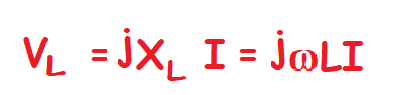
La representación igual que la anterior queda reflejada como puedes ver a continuación.
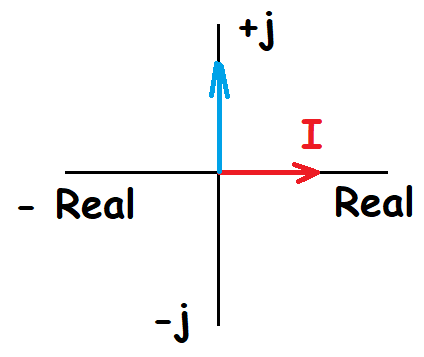
Impedancia.
De los circuitos anteriores hemos deducido que un condensador adelanta la intensidad respecto a la tensión y que una inductancia retrasa la intensidad respecto a la tensión. Entonces un circuito con inductancia y condensador, neutralizará las reactáncias y dejarán solo la resistencia, ¿verdad?.
El siguiente circuito muestra un condensador y una inductancia en serie con una fuente alterna. Se presentan las dos reactancias en el circuito por la presencia de los elementos pasivos.
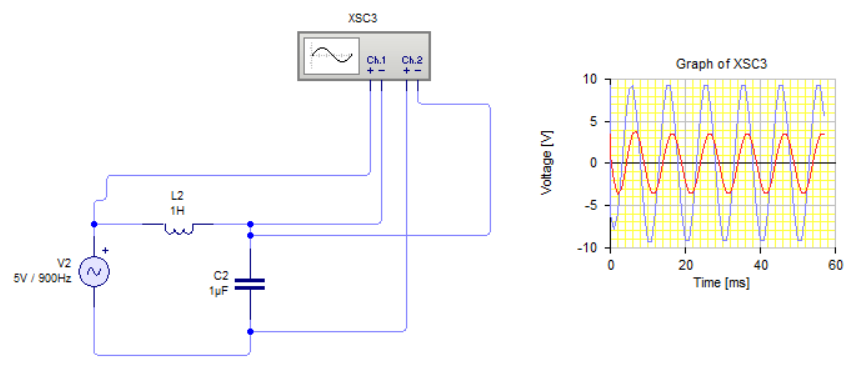
Dependiéndo del valor de las reactancias, el circuito se comportará como si solo tuviese condensador o inductancia. Las corrientes estarán desfasadas siempre entre si 90º, pero el adelanto de la una sobre la otra dependerá del valor de la reactancia total del circuito que se obtiene como suma algebraica de las reactancias capacitivas e inductivas.
Existe un caso particular que el valor de las reactancias son iguales (pero opuestas), y por lo tanto la reactancia total se anula. Como la reactancia es cero, la corriente por el circuito tiende a infinito y las caidas de tensión son iguales en ambos componentes. Este fenómeno se denomina resonancia.
Magnitudes de la reactancia total.La reactancia total se obtiene como resultado de sumar algebraicamente los valores de la reactancia capacitiva y la reactancia inductiva.

Según el valor modular la reactancia total se puede obtener como la resta de los módulos de las dos reactancias.
XT = XL - XC
El diagrama vectorial quedaría así:
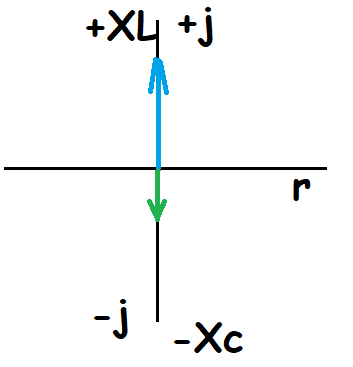
Como en el circuito no existen elementos resistivos, la potencia activa del circuito es nula. La potencia reactiva coincidirá con la potencia aparente de la resultante de la reactancia.
Impedancia.En un circuito como el siguiente, con condensador, inductancia y resistencia, si a la resultante de la reactancia le sumamos el valor de la resistencia, obtendremos un valor en ohmios. Dicho valor es la impedancia.
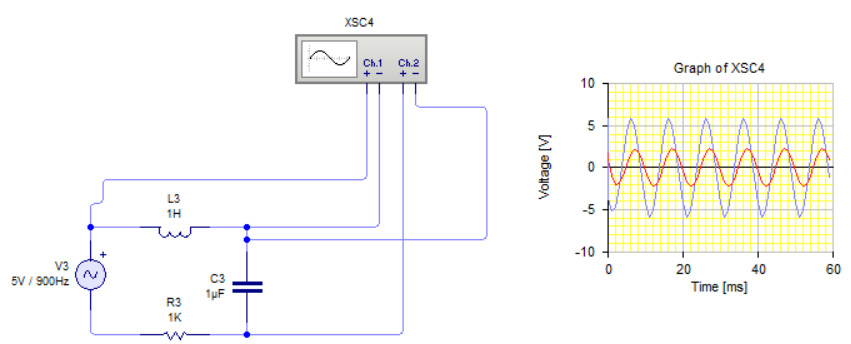
La impedancia se representa mediante la letra Z y como hemos dicho su valor en ohmios es la suma aritmética de las reactancias y la resistencia.
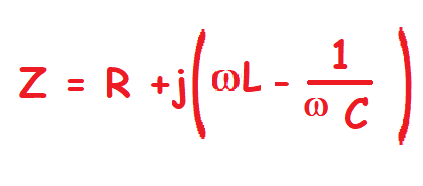
Para calcular el módulo y el argumento de la impedancia:
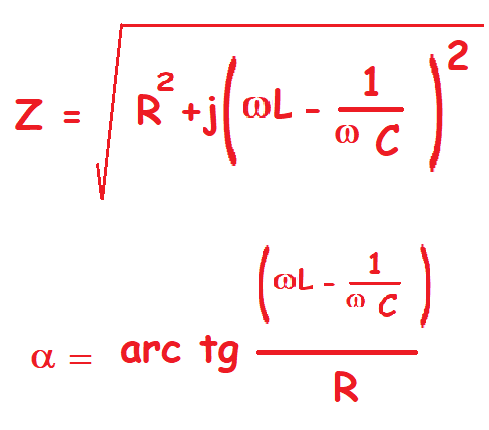
Puedes deducir de las anteriores fórmulas que la parte imaginaria de la impedancia depende de los valores relativos de las reactancias.
En el blog del canal de electrónica, puedes ver otra serie de prácticas como resolución de circuitos reactivos. Visita el blog desde el siguiente ENLACE.
Ahora puedes visitar el enlace del vídeo del capítulo.
