Pines analógicos.
Lo usual es que un registro digital u otras memorias digitales vinculadas con la computación o con las telecomunicaciones, tengan una capacidad de representación de informaciones de por ejemplo 8 bits, o 16 bits, o 32 bits, o 64 bits, etc.; una memoria binaria tiene una capacidad efectiva de representación de un bit.
El sistema decimal se basa en registros numerales de diez dígitos del 0 al 9, mientras que en un sistema binario (en base 2), solo se implican dos, el 0 y el 1.
Siempre tenemos referencia al sistema decimal, pero los ordenadores y sistemas electrónicos no entienden otros sistemas que los binarios, y cuando tienes que representar un número decimal en binario, aunque la representación sea similar, no significa lo mismo para un sistema u otro.
Por ejemplo, el número 10 en decimal significa diez unidades, pero en binario solo significa uno y cero. El número 1000, significa mil en decimal, pero en binario uno, cero, cero, cero. Ahora imagina números como 45903, 34800, etc., etc., que han de ser traducidos a binarios, porque ten en cuenta que el ordenador no va a entender el número 45903 si no lo traduces a su símil en unos y ceros. Para ello utilizamos unas tablas de traducción teniendo en cuenta la unidad del número decimal a traducir:
| 106 | 105 | 104 | 103 | 102 | 101 | 100 |
| 1000000 | 100000 | 10000 | 1000 | 100 | 10 | 1 |
Fíjate que cualquier potencia de 10 representa el número de ceros a la derecha que tiene del decimal 1 en binario. Cualquier número decimal cabe dentro de la tabla teniendo en cuenta el número de potencia que conlleva, es decir, por ejemplo, si el número es el 45903, sabemos que su potencia similar es 104 porque ocupa el mismo espacio que 10000. Traduciendo matemáticamente y extrapolando podemos decir que:
[4 * 10000] + [5 * 1000] + [9 * 100] + [0 * 10] + [1 * 3] = 45903
Pero para el sistema binario también existen unas tablas de traducción, aunque en este caso las potencias están en base 2.
| 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 |
NOTA: El rango de las tablas puede tener todas las potencias que quieras.
Así, por ejemplo, para calcular los unos y ceros que tiene un número decimal debemos de extrapolarlos a la tabla anterior de manera que no sobrepase la potencia máxima de la tabla. Por ejemplo, el número 108 decimal estaría dentro de la potencia de 26, ya que 26 es igual a 64 y este número cabe dentro de 108 (sin embargo, la potencia 27 no cabe dentro de 108 ya que es superior). Como 108 es mayor que el número de referencia, en la tabla va un 1 en la columna 26:
| 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 |
Como has tenido un TRUE, resta el número original a la potencia que te ha dado el valor, en este caso restamos 108 a 64 obteniendo 44. Bajando por la tabla, la siguiente potencia de referencia es 25. ¿El número 44 es mayor o igual a 32? Como 32 cabe en 44, la respuesta es TRUE por lo que en la columna de 25 se pone 1:
| 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 |
Al ser TRUE la respuesta volvemos a operar con el nuevo número: 44 – 32 = 12. Bajando a la siguiente columna 24, volvemos a hacernos la misma pregunta, ¿es 12 mayor o igual a 16? Ahora como la respuesta es negativa (FALSE), en la columna 24 se pone un cero porque 16 no cabe dentro de 12.
| 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 |
Como no hemos obtenido un TRUE solo pasamos a la columna siguiente (23) con el mismo número de referencia. ¿Es 12 mayor o igual a 8? Como la respuesta es positiva, en la columna 23 va un 1 y se procede a realizar la resta de 12 – 8 = 4
| 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 1 |
¿4 es mayor o igual a 22 (4)? TRUE entonces, 4 – 4 = 0.
| 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 1 | 1 |
¿Es 0 igual o mayor que 21? FALSE; entonces se pone cero en esta columna:
| 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
Y se sigue bajando por la escala. ¿Es cero mayor o igual que 20? FALSE; entonces se pone un cero:
| 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 |
Así que el número decimal 108 en binario es 1101100.
Bit o Byte.
El bit es la unidad mínima de comunicación que puede ser tratada por un sistema informático. Es un 1 o un 0.
En los sistemas, la comunicación se suele dar en paquetes de comunicación llamados byte y que son la unión de 8 bits, es decir por ejemplo el número binario 00011100.
Un bit se puede representar en el medio físico mediante un pulso de corriente o tensión; en ausencia de tensión, el bit puede ser FALSE o 0, y con presencia de tensión TRUE o 1.
Volviendo al principio del tema, cuando hablamos de que un puerto analógico tiene una resolución de 10 bits estamos hablando que podrá transportar informaciones de hasta 10 estados, siendo el mayor de ellos el número binario 1111111111 que se considera un paquete de datos. Los datos se pueden dividir en tramas que son partes de paquetes en la comunicación con el ordenador.
Así pues, si convertimos el número 11111111 a decimal obtenemos el número 255, y si traducimos los 10 bits 1111111111, obtenemos el número 1023.
Entradas analógicas.
Arduino UNO dispone de 6 entradas analógicas.

De lo dicho anteriormente cada puerto manejará un ancho de banda de 10 bits por puerto, lo que, en cifras manejables, por así decirlo significa que cuando se apliquen 5V a la entrada de un puerto, ese puerto manejará los 10 bits completos, es decir 1111111111 o lo que es lo mismo, un valor digital de 1023.
Por otro lado, si por el puerto no se aplica tensión alguna, corresponderá al valor cero o al número binario 0000000000.
Se puede modificar la tensión de entrada al puerto Arduino para establecer una tensión de referencia. Hasta ahora hemos considerado la tensión de referencia de 5 voltios para dispositivos que se conectan a los puertos analógicos. Pero puedes conectar dispositivos que requieran de más tensión como por ejemplo relés, inductivos, detectores, etc., etc.
Para cambiar la tensión de referencia se utilizará la función analogReference(); y se introducirá la nueva tensión por el pin AREF situado junto a los pines de entrada y salida digitales.

Resolución de las entradas analógicas.
Los valores que puede tomar las salidas analógicas siempre vendrán referenciados según la tensión de referencia y la cantidad de valores que puede tomar. Así si se conecta la placa Arduino a través del puerto USB del ordenador, la tensión de alimentación será de 5V. Entonces eso implica que cuando exista una entrada con la tensión de 5 voltios, corresponderá con un valor de 1023 mientras que sin tensión corresponderá al valor de 0.
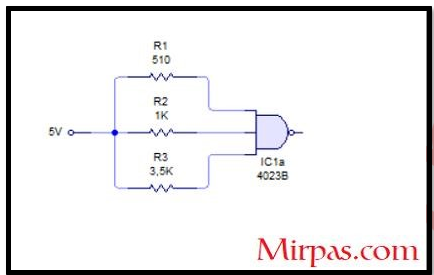
Supón un circuito conectado a una puerta lógica sumadora balanceada. El ramal R1 ofrecerá una corriente específica mayor que cualquiera de las otras dos. El ramal R3 ofrecerá la menor corriente, mientras que el ramal R2 tendrá una corriente superior a R y menor de R3. Por cada valor de ramal, la entrada analógica de Arduino devolverá un estado de bits en relación a la tensión específica.
Conversión analógica - digital.
Una señal eléctrica analógica es aquella en la que los valores de la tensión o voltaje varían constantemente y pueden tomar cualquier valor. En el caso de la corriente alterna, la señal analógica incrementa su valor con signo eléctrico positivo (+) durante medio ciclo y disminuye a continuación con signo eléctrico negativo (–) en el medio ciclo siguiente.
Un sistema de control (como un microcontrolador) no tiene capacidad alguna para trabajar con señales analógicas, de modo que necesita convertirlas en señales digitales para poder trabajar con ellas. Arduino UNO dispone de un conversor analógico - digital que proporciona la transformación de la señal analógica en su símil digital. Pero en la transformación se pierde información de acuerdo a la resolución de las entradas analógicas.
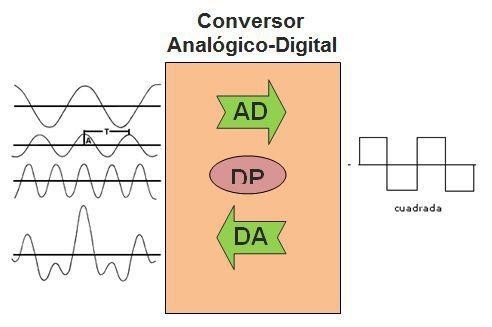
Ya hemos estudiado que con 5V, el convertidor analógico digital (ADC), transforma una señal analógica ocupando 10 bits de resolución. Es decir, teniendo una señal analógica, el ADC convierte el valor de tensión o corriente en pulso digital repartiendo los pulsos a lo largo de la resolución del puerto.
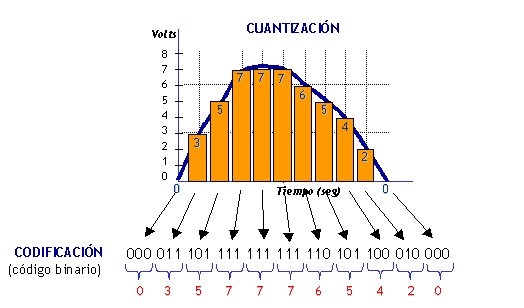
Mientras mayor sea la resolución del ADC, mayor será la reproducción de la señal analógica.
Resolución mejorada.
Como has visto, para una tensión dada que alimente una entrada analógica, el convertidor analógico digital administra el ancho de banda en cuestión estirando o retrayendo los valores de la señal para adaptarla a los 10 bits de resolución.
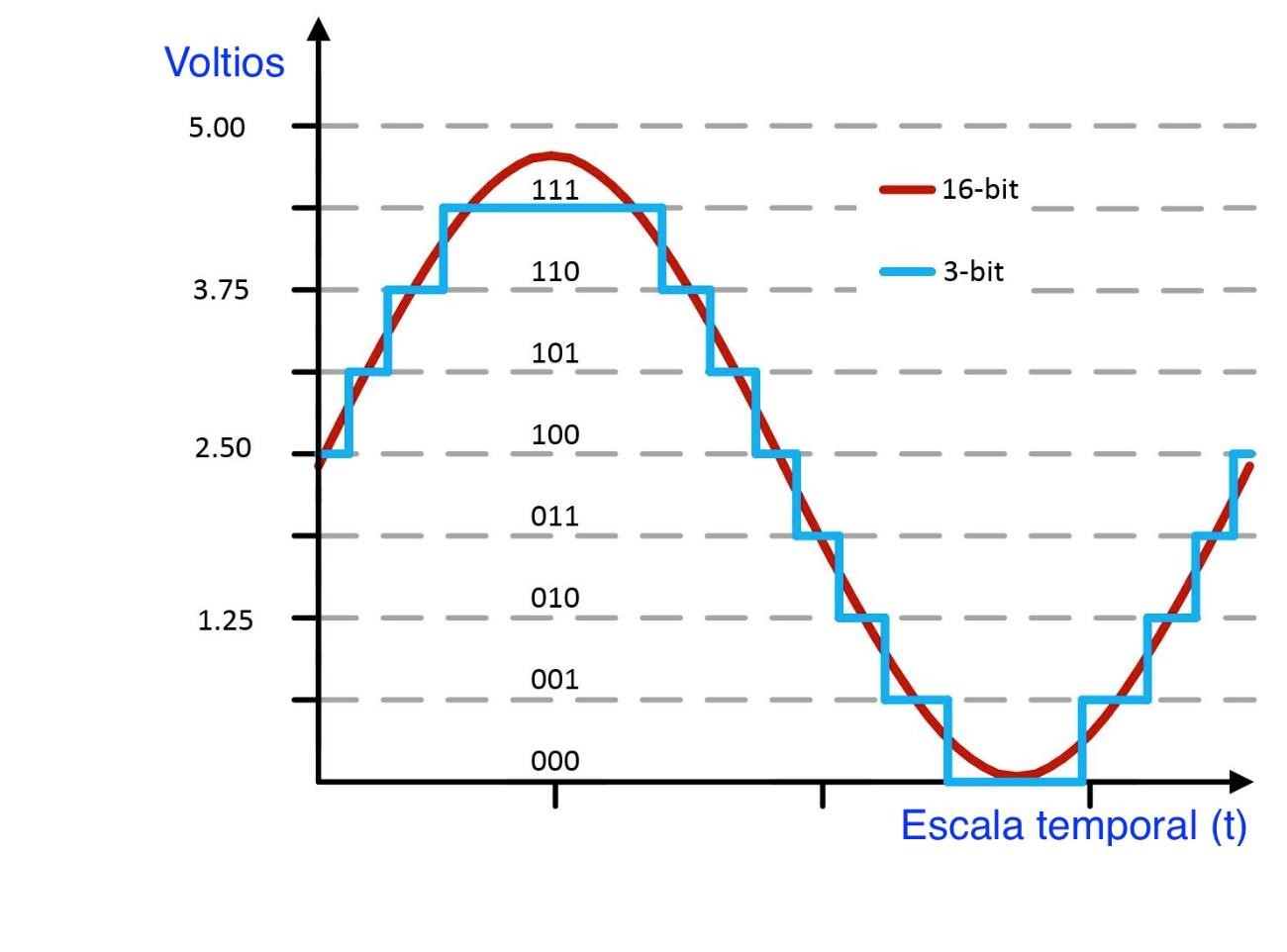
Por lo que, si en 5 voltios la señal debe de caber en 10 bits, implica que el ACD deba estirar la señal más produciéndose una pérdida de información que restará precisión a la medida. Para solucionarlo, en vez de utilizar la alimentación de 5V utiliza la del puerto de 3,3V de tu Arduino UNO.
Continuará en el siguiente capítulo.