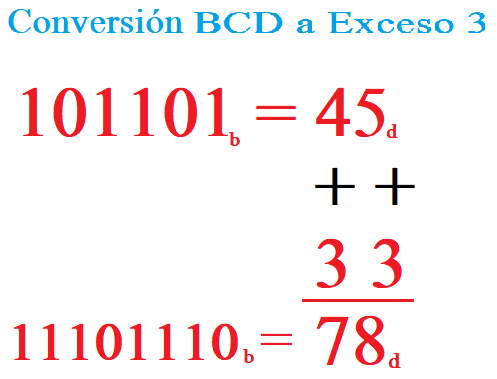Códigos en electrónica.
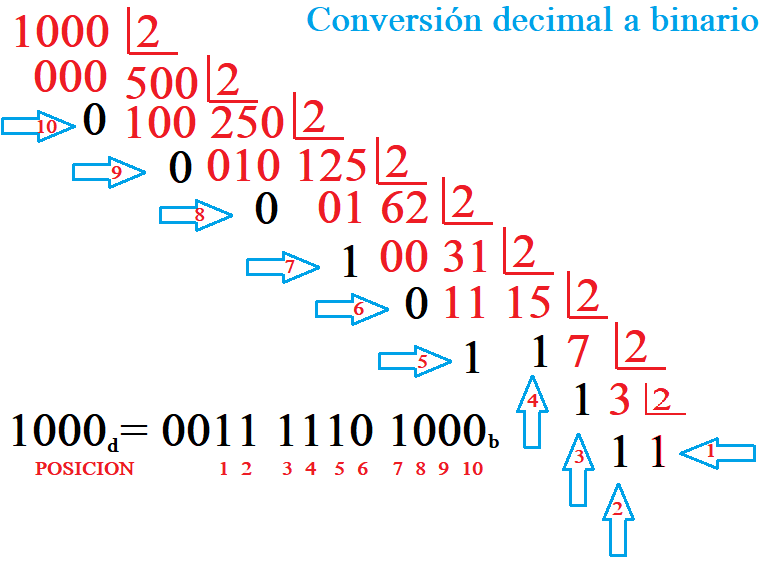
Para poder compartir la información que está en formato digital, es común usar representaciones binarias y hexadecimales para compartir dicha información. La más habitual es la codificación BCD (binary encoded decimal o Decimal codificado en binario).
Código BCD.
Ya hemos visto que un código binario es la forma de representación de información mediante dígitos binarios. El código BCD es un código muy usado en los sistemas de entrada y salida de datos en decimal, como por ejemplo un conversor.
Este código se basa en representar cada uno de los dígitos decimales (de una cantidad decimal), en sus correspondientes binario natural.
Así por ejemplo del número decimal 11, separaremos cada dígito en su correspondiente binario:
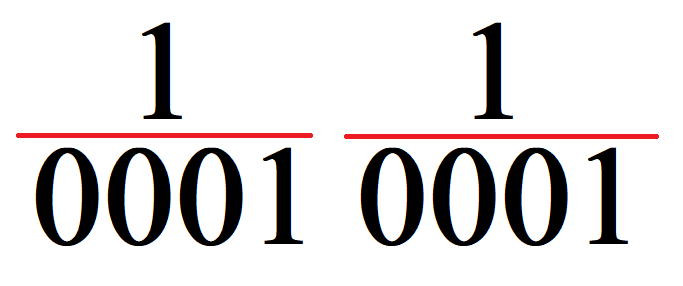
Pero ojo, no significa que el número decimal 11d sea el obtenido individualmente entre ambos dígitos (1011b)
Así pues, el número binario del decimal 11d, necesita de 8 bits para codificar dicho número a su equivalente binario. Sin embargo el número decimal 11d solo ocupa 4 bits en su equivalente binario (1011b), por lo que para codificar un número decimal de N dígitos se necesitan N grupos de 4 bits.
Así por ejemplo el número 1977 en código BCD es:
1d(0001b)9d (1001b)7d(0111b)7d (0111b)
NOTA: El código BCD es el que está entre paréntesis.
Aplicación práctica.Traducir al código BCD un código decimal nos servirá para convertir un valor decimal en una serie de pulsos eléctricos que actuarán sobre una entrada. Dicha salida la podremos controlar para que nos devuelva un número específico en un display de 7 segmentos. O también podemos controlar las entradas desde Python para que nos devuelva un número especifico en las salidas.
Puedes aprender más sobre ello Aquí.
La conversión a decimal desde BCD es bastante sencilla, porque simplemente tienes que hacer la unión de los números decimales en grupos de 4 bits. Por ejemplo vamos a ver el número anterior en BCD es:
0001 1001 0111 0111b
Sabemos que el 0001b es el número 1d; el número 1001b es el número 9d; el número 7d es el número 0111b y el otro digito faltante también es un 7. Por lo tanto el número 0001 1001 0111 0111b es igual al 1977d.
NOTA 2: Por si no lo has notado, cada número expresado tiene un sub índice que indica la base a la que pertenece siendo b de binario y d de decimal.
El código BCD tiene un "peso" (o ponderación de su valor) en que cada digito binario de 4 bits representa un código según esta ponderación. Entonces el código del BCD es el 8-4-2-1, porque por cada grupo de 4 bits representativos del número decimal, los digitos binarios del grupo representarán dicho código, me explico. Volvamos al número 1977.
0001 1001 0111 0111b
Si cogemos su primer grupo de 4 bits (0001) y lo extrapolamos al peso del código BCD, es decir 8-4-2-1, cada operación del dígito binario nos devolverá el valor del dígito decimal:
0001b = (8 x 0) + (4 x 0) + (2 x 0) + (1 x 1) = 1d
El siguiente grupo de 4 bits del código es:
1001b = (8 x 1) + (4 x 0) + (2 x 0) + (1 x 1) = 9d
Y los dos siguientes son:
0111b = (8 x 0) + (4 x 1) + (2 x 1) + (1 x 1) = 7d
0111b = (8 x 0) + (4 x 1) + (2 x 1) + (1 x 1) = 7d
La suma de los pesos del código BCD natural nos da un valor de 1-9-7-7 en decimal (1977d)
Codigo BCD Aiken.
El código BCD Aiken es un sistema de codificación parecido al BCD natural pero con los "pesos" distribuidos de una manera diferente al primero.
En esta codificación tenemos una ponderación de 2-4-2-1, por lo que cambia sensiblemente respecto al anterior, pero mantiene su geometría de los 4 bits ya que lo que hacemos es tener una referencia de los primeros 4 números decimales (a binarios de la forma igual) y los siguientes, hasta el 9, se ponen de forma simétrica a los anteriores.
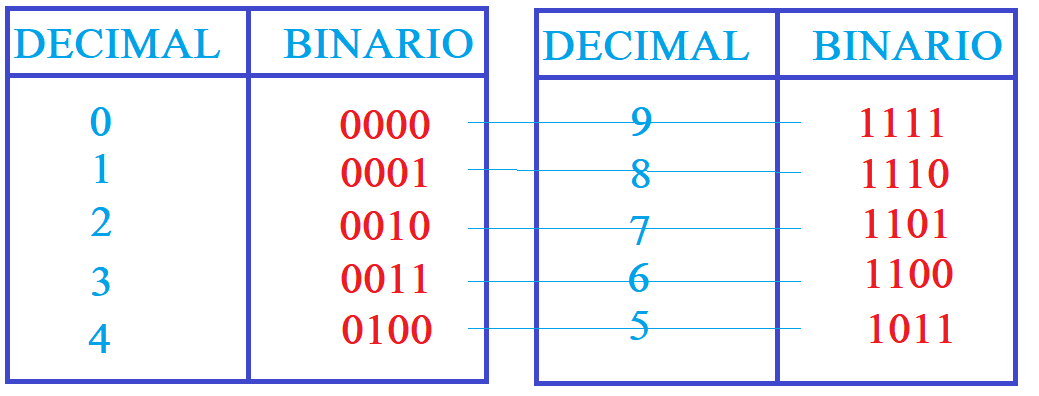
Como puedes ver en la anterior tabla, la codificación Aiken, los primeros números decimales del 0 al 4 se codifican según la tradicional habilitación de sus números binarios; pero de los números 4 al 9, la codificación binaria de estos decimales es de acuerdo a la simétrica de sus anteriores (contraria).
Veamoslo con un ejemplo. Siguiendo con el mismo número 0001 1111 1101 1101b, con el código Aiken establecemos la relación entre cada grupo de bits:
0001b = (2 x 0) + (4 x 0) + (2 x 0) + (1 x 1) = 1d
1111b = (2 x 1) + (4 x 1) + (2 x 1) + (1 x 1) = 9d
1101b = (2 x 1) + (4 x 1) + (2 x 0) + (1 x 1) = 7d
1101b = (2 x 1) + (4 x 1) + (2 x 0) + (1 x 1) = 7d
Fijate que curiosamente el número 0001 1111 1101 1101ben su transformación decimal según el código Aiken es el número 1977d. Y en su código natural es 0001 1001 0111 0111b que es el mismo decimal.
Este código es muy útil para operaciones de resta y división.
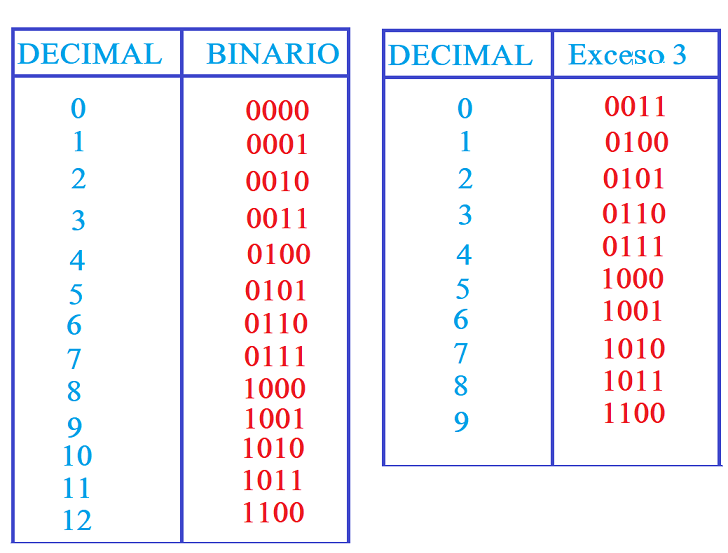
Código Exceso 3.
Este código es el más sencillo de usar ya que es muy similar al cifrado Cesar. Partiendo del código BCD natural, se realiza la suma de 3 al código habitual, así por ejemplo si el número 1d = 0001b, su número en exceso 3 será (1 + 3d) = 4d o lo que es lo mismo 0100b.
Para la codificación de cualquier número se procede igual que en el código BCD natural, agrupando los dígitos decimales en grupos de 4 bits como hemos hecho hasta ahora, pero en lugar de codificar en su código BCD natural, lo hacemos en su código exceso 3.
1977d
0100b 1101b 1010b 1010b
No tiene mayor complicación porque solo hay que sumar 3 dígitos al código BCD natural.
Código Gray.
El código Gray es un código especial no ponderado, es decir que los dígitos que lo componen no tienen un "peso" asignado. Con el código Gray puedes trabajar con el número de bits que quieras. Y la conversión de binario a Gray es muy sencilla si tienes en cuenta esto que te voy a indicar.
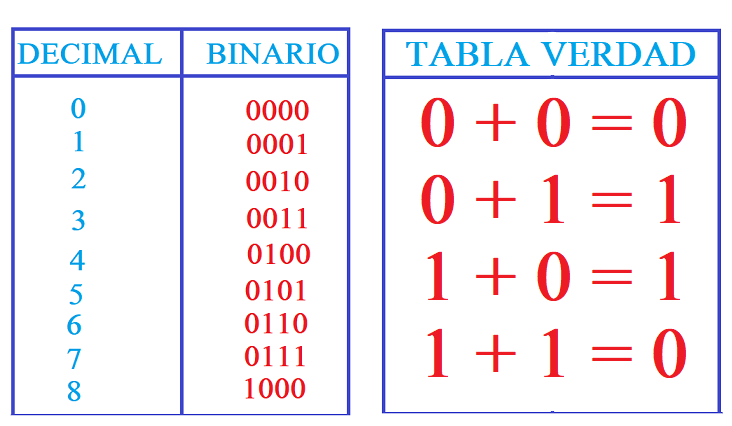
En la imagen superior puedes ver la tabla Gray a la derecha. Esta tabla es una tabla de verdad NAND que nos servirá para convertir binarios a código Gray.
Para convertir código binario a Gray simplemente tienes que seguir las dos reglas básicas:
● No se tienen en cuenta los acarreos de las sumas binarias.
● Siempre se tendrá en cuenta el bit más significativo de la suma (siendo esté el 1 más a la izquierda).
● De izquierda a derecha se realizará la suma binaria de cada dígito adyacente.
Vamos a hacer un par de ejemplos y verás qué fácil es. Cojamos los primeros 4 números binarios:
0000b
0001b
0010b
0011b
Del primer número 0000b, si sumamos sus dígitos (aunque no hay ninguno significativo), deberíamos de hacerlo teniendo en cuenta la tabla de verdad de Gray anterior y partiendo del primer dígito sobre la izquierda. Bajando ese cero:
0
0pos1 + 0pos2 = 0
0pos2 + 0pos3 = 0
0pos3 + 0pos4 = 0
Por lo que el código Gray para el 0000b es igual: 0000gray.
NOTA: Fijate que solo hemos sumado los tres primeros digitos. El cuarto se pone el primer carácter a la izquierda. Veamos el segundo número.
El 1d binario es 0001b, entonces sumando según la tabla Gray:
0
0pos1 + 0pos2 = 0
0pos2 + 0pos3 = 0
0pos3 + 1pos4 = 1
Por lo que el código Gray para el 0001b es igual a: 0001gray.
El 2d binario es 0010b, entonces sumando según la tabla Gray:
0
0pos1 + 0pos2 = 0
0pos2 + 1pos3 = 1
1pos3 + 0pos4 = 1
Por lo que el código Gray para el 0010b es igual a: 0011gray.
Para el 3d binario es 0011b, entonces sumando según la tabla Gray:
0
0pos1 + 0pos2 = 0
0pos2 + 1pos3 = 1
1pos3 + 1pos4 = 0
Por lo que el código Gray para el 0011b es igual a: 0010gray.
Para el 4d binario es 0100b, entonces sumando según la tabla Gray:
0
0pos1 + 1pos2 = 1
1pos2 + 0pos3 = 1
0pos3 + 0pos4 = 0
Por lo que el código Gray para el 0100b es igual a: 0110gray.
Y como el código no conlleva acarreo, podemos transformar todos los números que queramos a código Gray. Vamos a ver un último número:
100101b
1
1pos1 + 0pos2 = 1
0pos2 + 0pos3 = 0
0pos3 + 1pos4 = 1
1pos4 + 0pos5 = 1
0pos5 + 1pos6 = 1
El número más significativo a la izquierda es un 1, por lo que se pone antes del número en la primera posición. Por lo que el código Gray para el 100101b es igual a: 110111gray.
Código Hexadecimal.
El código hexadecimal es un código muy utilizado tanto en programación como en electrónica de control muy usado en la industria logística. El sistema hexadecimal es un sistema en base 16, es decir que tiene 16 caracteres significativos. Y es un sistema más cercano a los sistemas de comunicación y relacionados con los lenguajes y su alfabeto.
Pero el sistema hexadecimal no está formado solo por números como los sistemas que hemos visto hasta ahora, sino que también lo conforman letras. Así el sistema hexadecimal está compuesto por los siguientes caracteres:
0 1 2 3 4 5 6 7 8 9 A B C D E F
Las letras en sí no representan lo explícito, sino que viene a significar que cada una representa para el código fuente su representación fictícia, es decir la letra A = 10; la B = 11, etc., hasta llegar a la F = 15. En total 16 caracteres.
Para convertir un número hexadecimal a decimal partiremos de nuestra tabla de potencias.

Puedes ver que las letras en realidad representan sus equivalentes de valores respecto a la tabla decimal. Vamos a coger un número por ejemplo el 35616.
Para realizar la conversión del número hexadecimal a decimal, empezando por la derecha es tan fácil como ir poniendo las potencias encima del número (como haciamos con los binarios), pero teniendo en cuenta que la base es 16 en lugar de 2.
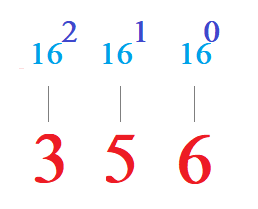
Si hubiese más números a la derecha se van poniendo las siguientes potencias de 163, 164,....,16N, hasta completar el número de carácteres del número.
Convertir números de hexadecimal a decimal es tan fácil como multiplicar el resultado de la potencia encima del número por el propio número. Me explico:
162 = 256 x 3 = 768
161 = 16 x 5 = 80
160 = 1 x 6 = 6
Si sumamos los tres números nos dará el valor de 854d
Veamos otro número, el 2F:
161 = 16 x 2 = 32
160 = 1 x 15 = 15
La suma nos devuelve el número 47d
Fijate que ahora el valor "F" lo hemos sustituido por el valor literal, es decir el 15.
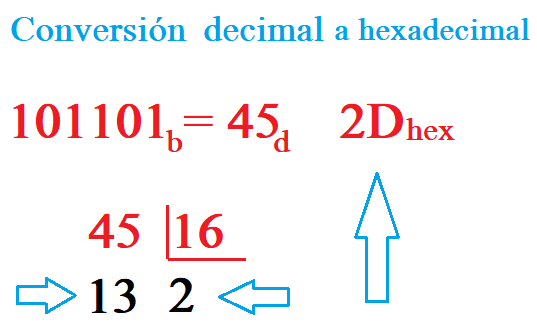
Para convertir de decimal a hexadecimal, tenemos que dividir los números entre 16 hasta no poder dividir los cocientes más (al igual que en binario). Vamos a convertir el número 555d a hexadecimal. A continuación te muestro el proceso.
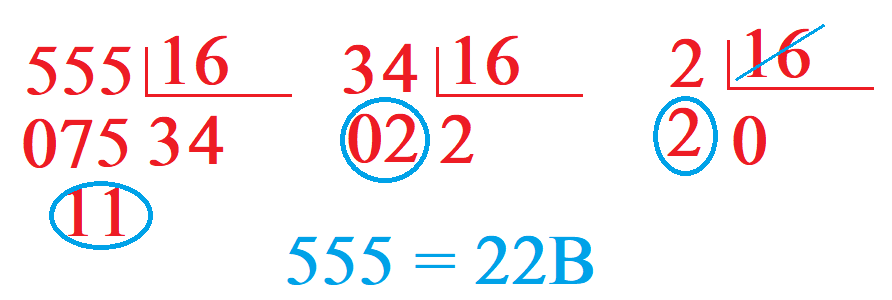
Fijate que para crear el hexadecimal cogemos de derechas a izquierda la creación del número. Y sustituimos el 11 por su letra equivalente.
Ejercicios propuestos.
Todo técnico en electrónica debe de ser capaz de transformar los números en diferentes codigos pues es el lenguaje máquina que gobierna la electrónica y la programación. Tomate tu tiempo para prácticar haciendo las siguientes conversiones. El subíndice te indica la base de los números:
● 100010 ------> ?2
● 1100102------> ?10
● 10110110------> ?16
● 3E816 ------> ?10
● 101101BCD---> ?exceso3
Gracias por compartir y ayudar a que mi proyecto siga creciendo y ganando subcriptores. Te lo agradezco.