Cálculo de inductancias.

Las inductancias o bobinas, son dispositivos electromagnéticos que generan una repulsión momentánea al paso de la corriente eléctrica generando una fuerza contra electro motriz. En este tutorial, aprenderás a calcular sus valores dependiendo de su constitución.

Bobinas de una sola capa.

Cuando digo de una sola capa, me estoy refiriendo a un único conductor bobinado, y no a las bobinas toroidales o los transformadores que tienen varias capas, como también a los dispositivos de acoplamiento magnético. En este tutorial solo veremos las bobinas de núcleo de aire que puedes hacer con cable de cobre.

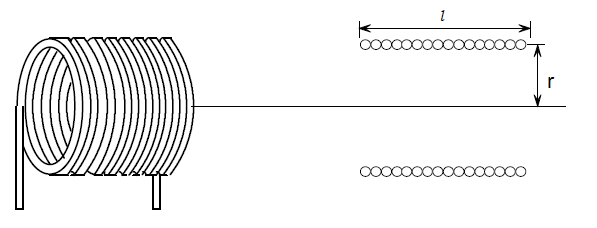
De cursos como el que tengo a tu disposición en la página principal de electrónica para newbies puedes ver los fenómenos a los que está enfrentado una bobina cuando circula corriente eléctrica alterna. De hecho sabemos que es lo que pasará, cómo pasará y porqué. Pero a veces al técnico le cuesta entender el proceso del cálculo de una inductancia.

En el cálculo de una inductancia, el cálculo será un valor real pero aproximado, ya que la fórmula se basa en propiedades físicas que son muy difíciles de predecir como el efecto de campos magnéticos externos al de la propia bobina, efectos resistivos, efectos capacitivos, resistividad del material, conductividad, resistencia, efecto skin y pérdidas por corrientes de Foucault e histéresis.

Para el caso de una bobina convencional, en la cual las espiras están separadas entre sí a una distancia infinitesimal, la inductancia viene definida por la fórmula siguiente:

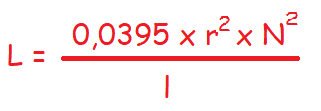
En donde:

Tanto r, como l vienen dado en centímetros. Y el valor de la inductancia viene dado en micro Henrios (µH).

Casos específicos.

Suele ocurrir al igual que cualquier otro componente que sus dimensiones modifican la estructura y el cálculo del sistema. Si divides el radio de la inductancia entre la longitud de la misma y el valor que te dé es mayor de 1, entonces hay que aplicar un factor de corrección que se dice, factor K, o constante de Nagaoka (que depende de la permeabilidad del sistema, la constitución de la bobina y el material del mismo).

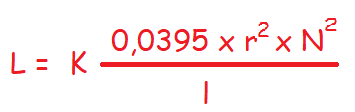
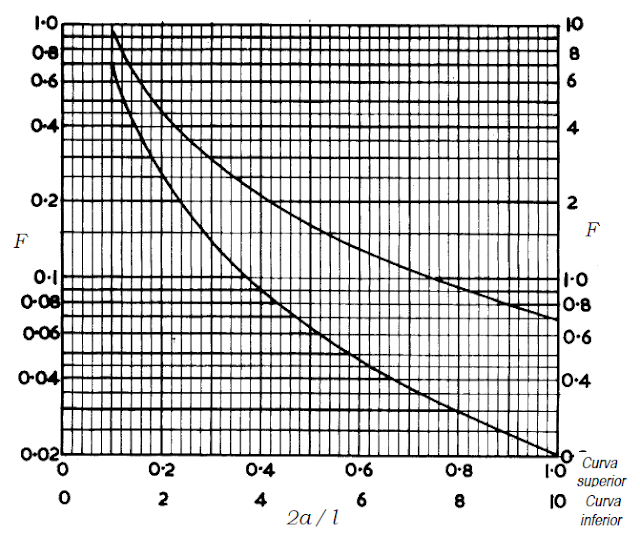
Como el desarrollo del cálculo de la constante es un tanto complicado, se usan gráficas para el cálculo de la constante de Nagaoka.

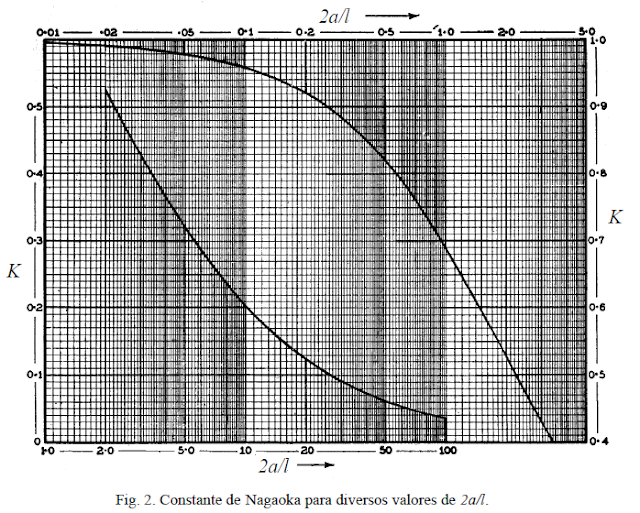
Por ejemplo en el anterior gráfico, supón una bobina de radio 0,5cm y longitud 1cm. Eso implicará un factor de (2)0,5/1 = 1. Lo que implica que en este caso no habría que aplicar el factor de Nagaoka. Pero para valores de K>1, si hay que aplicarlos.

Método sencillo.

La fórmula anterior produce variaciones en el cálculo del 1% sobre el valor real, lo que implica que introduce un error de un 1%. Existe una fórmula más directa para calcular la inductancia de una bobina y es gracias a la fórmula de Wheeler.

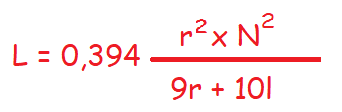
La fórmula anterior produce el mismo porcentaje de error del 1% pero aumenta el rango de la constante de Nagaoka ya que ese valor del 1% se mantiene entre valores comprendidos entre el los valores inferiores de 2r/l <1 y 2r/l =3; mientras que hasta valores de 2r/l = 5 se mantendrá un porcentaje de error del 4%. Y teniendo en cuenta la variación de la fórmula indicada por Esnault-Pelteire que usan un valor específico de K, nos queda:

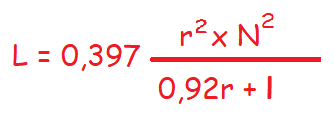
Que disminuye el error de cálculo al 0,1% para valores de 2r/l comprendidos entre los 0,2 y los 1,5. Esta fórmula es la que más se usa debido al bajo margen de error que genera en comparación con las otras fórmulas.

Caso práctico.

Si, está muy bien el hecho de la formulación teórica pero, ¿porqué no la llevamos a práctica ya que este blog es de prácticas de electrónica?

Hasta ahora hemos considerado la bobina según su diámetro, su longitud, la constante de Nagaoka y el número de vueltas, pero existen otros factores como el constitutivo que es el grosor del conductor y que es parte importante del problema. De hecho, mientras mayor sea el grosor del conductor bobinado, peor será la constante de Nagaoka y mayor será la perdida del valor de la inductancia.

Lo primero que se necesita conocer es el factor de forma.

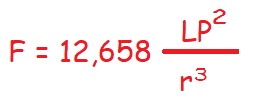
Siendo:

● L, la inductancia en micro Henrios.
● P, el paso entre bobinas.

Además conociendo la longitud y el paso de la bobina, se puede calcular el número de espiras:

Así que ahora podemos realizar cálculos para conocer las inductancias de acuerdo a las propiedades físicas de una bobina.

Queremos conseguir una inductancia de 5µH que se devanará de forma cilíndrica (utilizando un boli) con un diámetro de 8mm con un alambre de cobre de 0,05mm de grosor y las espiras juntas unas a otras:

● L = 5µH
● 2r = 0,8cm
● P = 0,05cm

Primero calculamos el factor de forma con la anterior fórmula para obtener un valor de 2,45. Ahora ese valor lo tenemos que llevar a la gráfica anterior del factor de forma que relaciona la ecuación 2r÷l para obtener el valor en la parte superior derecha de 0,36, tal como muestra el gráfico anterior.

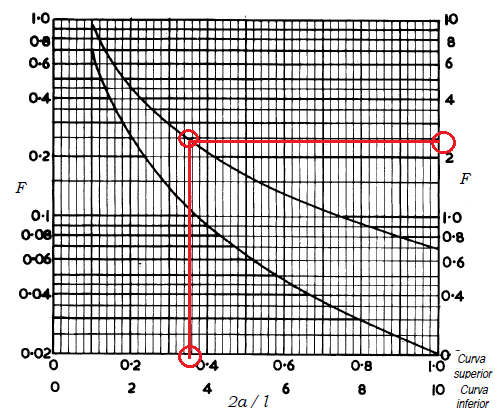
Ahora para calcular la longitud de la bobina, de la fórmula 2r ÷ l = 0,36, derivamos para obtener que l = 2r ÷ 0,36, lo que implica que si 2r = 0,8cm, entonces l será 2,22cm.

Para terminar, se calcula el número de vueltas que debe de tener el arrollamiento que relaciona la longitud de la bobina con el grosor de la misma:

N = l ÷ P = 2,22cm ÷ 0,05cm = 44,44 vueltas.

Por lo tanto ya has comprobado como calcular la inductancia que produce un inductor de cierta longitud, amplitud y grosor de acuerdo a las propiedades físicas aparentes.

Gracias por tu visita.