ELECTRÓNICA AVANZADA.

Mapa de Karnaugh.

Si recordamos los pasos que se han de seguir hasta la obtención del circuito con puertas lógicas de la clase anterior, obtendremos procedimientos que se deben de seguir para el diseño de los circuitos combinacionales.

Los circuitos combinacionales son aquellos en los que las salidas dependen unicamente del valor de las entradas. En dichos circuitos, por tanto, una misma combinación de entradas provocarán una misma salida.

Los pasos a seguir para el diseño de circuitos son:

● Construcción de la tabla de verdad a partir del enunciado del problema.
● Obtención de las ecuaciones lógicas por Minterm y Maxterm.
● Simplificación de las funciones por Boole o Karnaugh.
● Implementación del circuito con distintos tipos de puertas (o un solo tipo), aplicando la ley de Morgan.

En los ejemplos que veremos en esta clase, los circuitos podrán disponer de varias salidas. A dichos circuitos se les llama circuitos multifunción ya que están definidas por varias funciones (una por salida).

En el proceso de simplificación, es importante buscar términos cómunes a más de una función para utilizar menos puertas lógicas en la construcción del circuito. Y a la hora de diseñar la tabla de la verdad, puede ocurrir que determinadas combinaciones de entrada no puedan reproducirse o no tengan relevancia, y por tanto no esté definido el valor que se debe adoptar a la salida en dicho caso; entonces a la columna correspondiente se marcan dichas combinaciones con la letra X (salida indiferente). A la función obtenida se denomina función incompletamente especificada. Al rellenar el mapa de Karnaugh para realizar la simplificación deben indicarse dichas X, que podrán ser tomadas o no al realizar los lazos, dependiendo de si favorecen la máxima simplificación.

Mapa de Karnaugh.

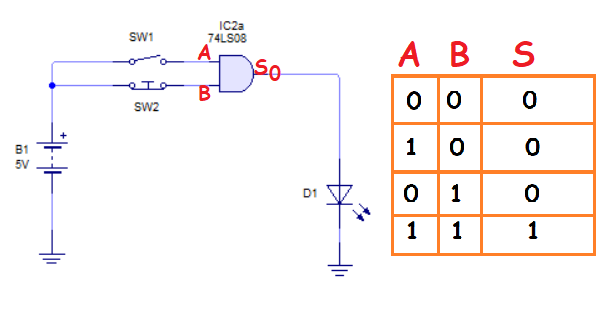
Supón el siguiente circuito simple con dos entradas A y B que devuelven una tabla de verdad como la representada en la imagen. Si queremos hacer el mapa de Karnaugh teniendo estas dos entradas, para ello representamos las entradas por el vértice superior izquierdo en un cuadrado de tantas filas y columnas como entradas tenga. En este caso dos filas y dos columnas.

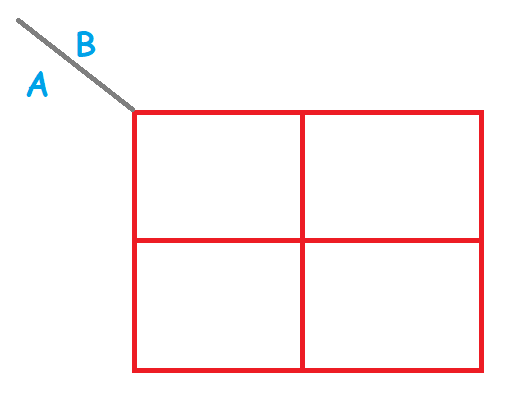
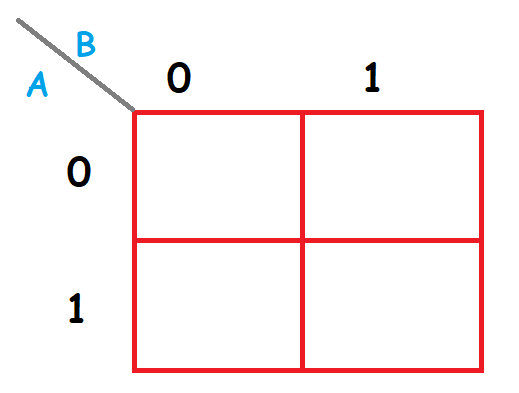
Como puedes ver en el vértice de entrada, las entradas se posicionan según van entrando en la tabla de verdad. Desde el punto de vista de la B, las columnas van a representar los valores que tendrá cada salida posible. Como solo hay dos estados posibles, la primera columna valdrá cero y la segunda columna valdrá uno. Desde el punto de vista de A, las filas también cogerán los valores posibles de las salidas, por lo que al haber solo dos estados, la primera fila valdrá cero, y la segunda fila valdrá uno. Esto es una representación básica del mapeo que hay que rellenar con los valores de la tabla de verdad.

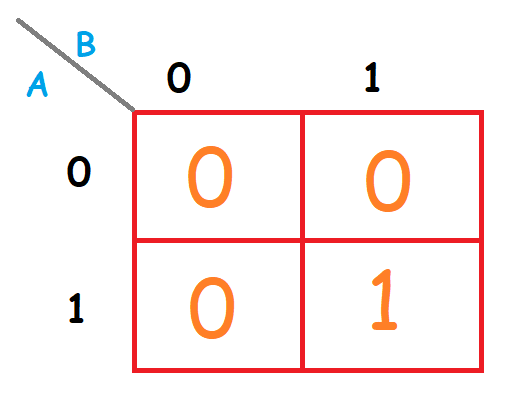
Ahora para rellenar los valores correspondientes en el mapa de Karnaugh, tienes que ver en la tabla de la verdad los registros. Si A es cero y B es cero, devuelve un cero. En la tabla de Karnaugh la fila marcada por cero y la columna marcada por cero, entonces valdrá cero. El segundo registro de la tabla de la verdad A vale uno y B vale cero devuelve una salida de cero; en el mapa de Karnaugh, la fila uno, y la columna cero, entonces tendrá el valor de cero. El tercer registro A vale cero, y B vale uno, devolviendo un cero; en el mapa Karnaugh, la fila cero y la columna 1 tendrá el valor de cero. Para terminar el registro A vale 1uno y el B vale uno, devolverá una salida uno; en el mapa de Karnaugh, en la fila uno y la columna uno, hay que poner un uno como se ve en la imagen siguiente.

Si queremos hacer el mapa de una función triple como la siguiente:

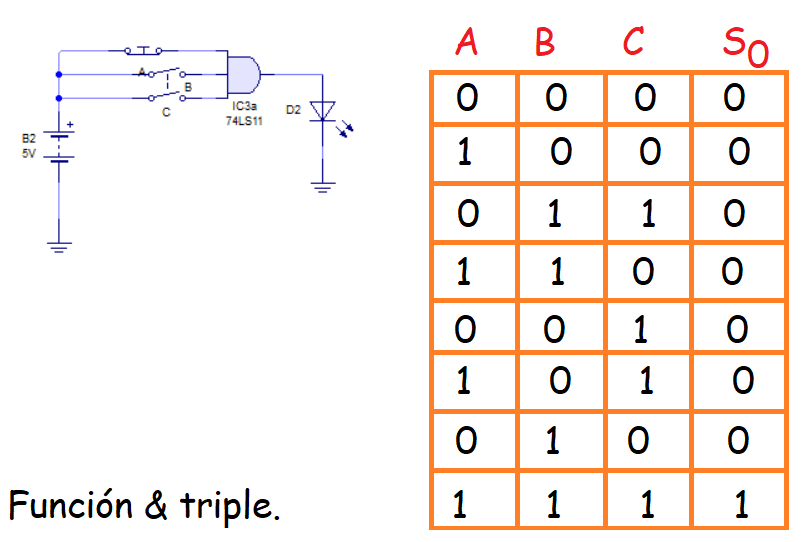
Tendríamos que hacer una tabla con ocho campos (ya que hay ocho posibilidades). Además como existen 3 entradas tendremos que agrupar dos entradas como si fuesen una sola, tal cual puedes ver en la imagen.

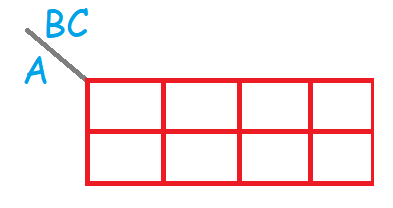
Como la entrada A solo va a tener dos posibles estados 0 y 1, se pone como filas.

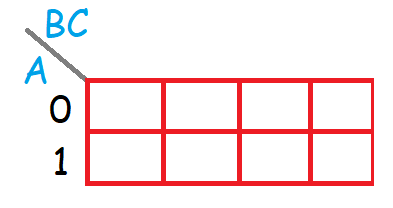
Pero la cosa cambia con los estados de la salida A y C, ya que pueden tomar varios valores para cada valor de sus entradas. Pueden tomar los siguientes valores:

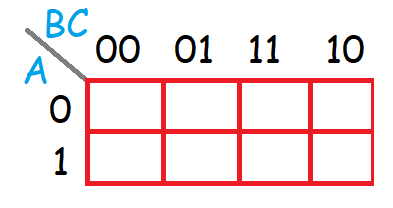
Como es una función AND el resultado es fácil de calcular ya que solo va a existir un uno en el campo 1-11, mientras que el resto de campos serán cero.

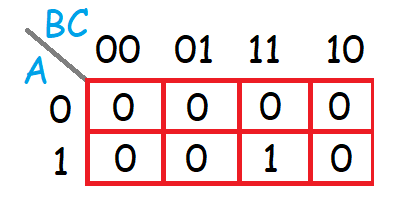
Los mapas de Karnaugh más utilizados son los de 3 y 4 variables, ya que para circuitos combinacionales de mas variables, la resolución se hace más caótica y se requieren de otros métodos como el de Quine-McCluskey.

En un mapa de Karnaugh de 4 variables, las variables de la tabla estarán divididas entre 16 campos de forma que los índices de las filas y las columnas sean los mismos que los índices de las columnas del tipo3 anterior:

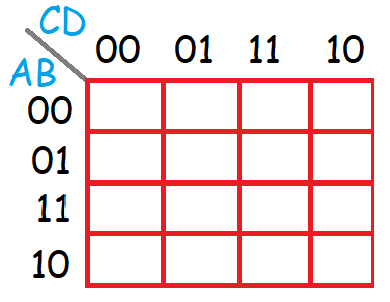
Ahora solamente queda reducir el circuito según el método de simplificación seguiendo las normas de agrupación de unos (pero no es el objetivo de este curso).

Decodificadores.

Los decodificadores son circuitos combinacionales construidos a partir de puertas lógicas y que tienen como finalidad activar una y solo una de sus salidas, dependiendo del valor que adopten sus entradas. Se dice entonces que los decodificadores convierten código de tipo binario, como el BCD, Binario puro, XS3, Gray, etc., en código decimal.

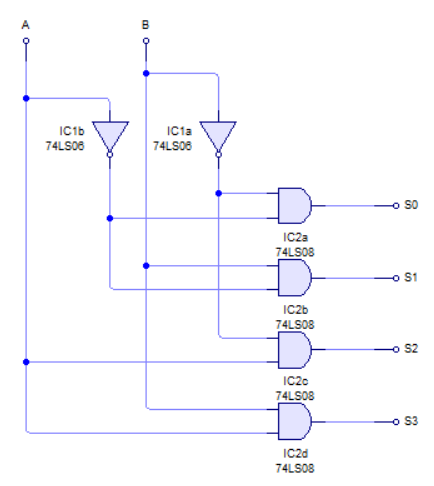
Podemos construir decodificadores de 1 a 2 líneas, de 2 a 4, de 3 a 8, 4 a 16, etc., siguiendo los mismo procedimientos usados para las puertas lógicas del anterior capítulo. Así por ejemplo para decodificadores de 2 a 4 líneas tenemos una tabla de verdad siguiente:

Las funciones de salida de dicha tabla están definidas por las fórmulas:

S0 = !A x !B
S1 = !A x B
S2 = A x !B
S3 = A x B

NOTA: El simbolo ! indica que la entrada es negada.

El circuito queda representado como se ve a continuación:

Comercialmente pueden encontrarse una gran cantidad de decodificadores en forma de circuitos integrados. Pero cabe destacar el 74LS47 que es un decodificador muy usado en prácticas y en la industria que sirve para conectar un display de 7 segmentos (Visita la práctica AQUÍ).

Insertando cuatro interruptores en el dispositivo somos capaces de producir una salida de números decimales con unas entradas binarias de unos y ceros. Según el estado de las entradas obtendremos una salida en cuestión formateada según la codificación del decodificador a decimal.

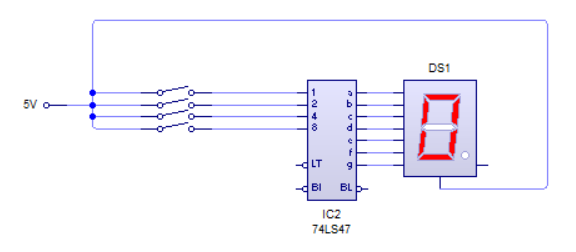
Como puedes ver éste decodificador convierte una señal binaria a una señal decimal que puede ser representado en un display de 7 segmentos. Este decodificador es un decodificador con lógica negativa, por lo que el display debe de ser de cátodo común. Además el decodificador 7447 dispone de una entrada LT (Lamp Test) para comprobar el estado del display, y de las señales BI/RBO y RBI utilizadas para unir varios displays en cascada y para que no se representen los ceros a la izquierda.

Codificadores.

Si los circuitos descodificadores convierten un número binario a decimal, los codificadores hacen lo inverso: convierten un número decimal en un número binario.

Los codificadores pueden ser de prioridad no sin prioridad. En los segundos solo debe de activarse simultáneamente una entrada. En caso contrario, la salida obtenida podría no corresponder con el número deseado. Cuando se activa más de una entrada en los codificadores con prioridad, se obtendrá en la salida la combinación binaria correspondiente al número de mayor prioridad, normalmente el de mayor valor.

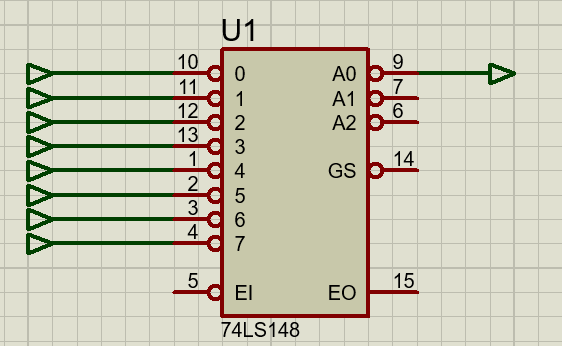
El mejor ejemplo de codificador comercial es el 74LS148 que es un codificador con 3 a 8 líneas con prioridad. Consta, además de las ocho entradas para el número a modificar, que trabajan en lógica negativa, de una entrada de inhibición, que pone las salidas a nivel alto cuando encuentra un uno. Las tres salidas del número codificado también trabajan en lógica negada. Además, dispone de dos salidas adicionales E0 que indica si todas las entradas están inversas y GS que se activan si una o más entradas están a nivel bajo.

Multiplexores y demultiplexores.

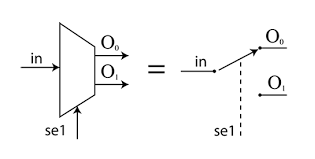
Los multiplexores son circuitos combinacionales que disponen de entradas de datos, entradas de selección y una única salida. Permiten enviar por una única línea (serie o bus de datos), los datos presentes en varias líneas (paralelo). En la línea de salida tendremos una señal aplicada a la entrada de datos elegida mediante las líneas de selección. Si se cambia el estado de las líneas de selección, una nueva entrada de datos quedará unida a la salida del circuito. El multiplexor se comporta como un conmutador de varias entradas y una salida, donde las líneas de selección gobierna la posición del mismo.

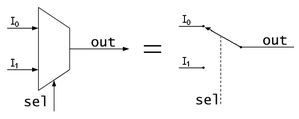
Se pueden encontrar multiplexores de 2 a una línea como el mostrado en la imagen superior; o de 4 a 1, de 8 a 1, etc., etc. Entre los más conocidos está el 74151 que es un multiplexor de 8 a 1 líneas, con lo que dispone de 8 entradas y una salida en lógica positiva Y, y otra en lógica negada W. También tiene tres líneas de selección y una entrada de inhibición activa a nivel bajo. La combinación binaria de las líneas de selección determina la línea de entrada que quedará aplicada a la salida del circuito.

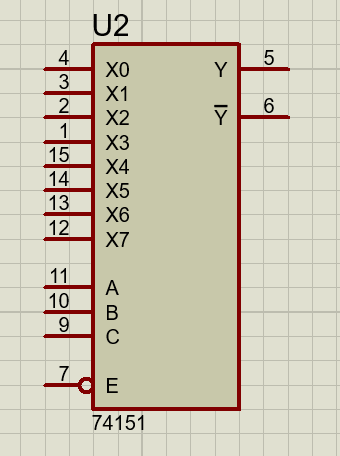
Los demultiplexores son circuitos combinacionales que realizan la función opuesta a los multiplexores; constan de una única entrada y varias salidas. Mediante las entradas de selección se elige en qué salida se obtiene la señal de entrada.

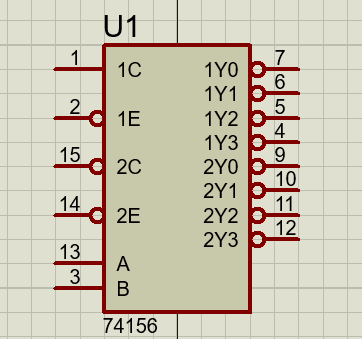
Como integrados populares de este tipo puedo indicar el decodificador-demultiplexor 74156, que puede trabajar como doble demultiplexor de 1 a 4 líneas con entradas A y B comunes; o como un demultiplexor de 1 a 8 líneas uniendo las líneas de datos 1C y 2C para formar la tercera entrada de selección y los strobes 2C y 2G que serán la entrada del dato.

Comparadores.

Estos son circuitos combinacionales que comparan dos combinaciones binarias presentes en sus entradas e indican si son iguales o no. Si son iguales, indica cual es mayor.

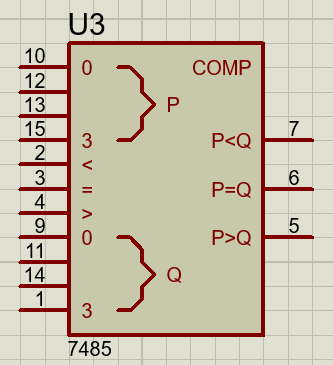
La imagen anterior muestra un circuito integrado 7485 que compara dos números binarios de 4 bits presentes en las entradas 10 - 15 a 2 - 9. Como puedes ver dispone de tres salidas para indicar el resultado de la comparación < o = o >. Además tiene tres salidas auxiliares para formar comparaciones de mayor número de bits.

Para formar comparadores mayores se suelen unir las salidas de un comparador 7485, al cual se aplican los bits de mayor peso, con las entradas auxiliares del mismo nombre del comparador 7485 que tendrá los bits menos significativos. La salida se tomará en éste último comparador.