Electrónica digital.
La electrónica se encuentra dividida en dos grandes grupos: La electrónica analógica, que varía sus parámetros de tensión y corriente de acuerdo a unos valores instantáneos en magnitud temporal. Y la electrónica digital esta caracterizada en que solo tiene en cuenta sus variaciones incrementales a partir de cierta magnitud de corriente o tensión.
Dependiendo de los tipos de componentes utilizados para fabricar elementos que forman la electrónica digital (puertas, sumadores, biestables, contadores, etc.,etc.), podemos encontrar diferentes familias lógicas, siendo las dos fundamentales la familia TTL y la familia CMOS.
La primera familia utiliza transistores bipolares y resistencias, mientras que la segunda familia utiliza transistores CMOS de las que más adelante veremos en detalle.
Los dos posibles niveles que pueden tener ambas familias son conocidos como estados lógicos; así el estado cero o lógico 0 es un bajo nivel de inactividad o tensión mínima comprendida entre 0 y 0,8V, estado de polarización inferior al de trabajo de un semiconductor. El estado lógico 1 o nivel alto, es el nivel activo de la señal y representa a una tensión máxima de entre 2 y 5V.
Existe también una lógica negada en el que el nivel activo es el 0 y el nivel inactivo es 1.
La electrónica digital también se encuentra dividida en dos grandes grupos: Los circuitos combinacionales, en los que la salida o salidas dependen unicamente de las entradas o entrada. Los circuitos secuenciales, la salida/s depende del estado de las entradas y además, de los estados anteriores del circuito por lo que la salida no tiene que adoptar el mismo estado que la entrada.
Dentro de la electrónica digital se puede diferenciar la lógica cableada y la lógica programada. En la primera, los elementos que forman el circuito están unidos mediante conductores eléctricos. Para modificar el circuito es necesario modificar el cableado y las conexiones. En la segunda, existen componentes donde se deposita un programa que indica la función que debe de realizar el circuito; para cambiar la función del circuito, solo hace falta modificar el programa.
Aprenderemos a utilizar y programar circuitos eléctricos en el curso de automatas programables.
Para terminar esta introducción, los componentes de los circuitos digitales aparecen en forma de circuitos integrados. Tomándo como unidad la puerta lógica (elemento básico de electrónica digital), podemos establecer dicho circuitos en cuatro niveles:
- SSI. Pequeña escala de integración entre 1 y 12 puertas.
- LSI. Media escala de integración entre 12 y 100 puertas lógicas.
- LSI. Alta escala de integración de entre 100 a 1000 puertas lógicas.
- VLSI. Muy alta escala de integración de mayor de 1000 puertas lógicas.
En la actualidad, todos los circuitos (sino al 90% de los circuitos del mercado), son digitales o tienen componentes digitales y el futuro es digital.
Sistema binario.
En la electrónica digital se pueden dar dos estados 1 y 0. Si tuviesemos que representar el número 2 con estos dos valores, no podríamos expresarlo en nuestra notación decimal, porque la electrónica digital solo utiliza dos valores como es el alto y bajo. Así que necesitariamos un código para representar valores decimales en codigo binario.
No me voy a enrrollar como hacen en otras páginas y cursos:
Convertir número decimal a base:Convertir un número decimal (en base 10) a cualquier otro tipo de base, por ejemplo base 2, solo hay que dividir dicho número entre la base a la que se quiere obtener.
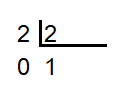
En la imagen anterior has visto que la división resultante devuelve un resto de 0 y un cociente de 1. Siempre hay que coger el último cociente y después los restos de la división para obtener el número de dicha base. En nuestro caso el número decimal 2, se convierte en el número binario 01 (no uno, sino cero, uno).
Codificación.Cuando hablamos de codificación me estoy refiriendo a que en la situación anterior, el número 2 en binario se representa de igual manera que el número 1 que está en base decimal. Entonces, había que representar los números en función de su base y en función de su valor representado.
En electrónica digital se hace uso de distintos códigos que muestro a continuación en la siguiente tabla:
| Decimal | BCD | AIKEN | XS3 | GRAY |
| 0 | 0000 | 0000 | 0011 | 0000 |
| 1 | 0001 | 0001 | 0100 | 0001 |
| 2 | 0010 | 0010 | 0101 | 0011 |
| 3 | 0011 | 0011 | 0110 | 0010 |
| 4 | 0100 | 0100 | 0111 | 0110 |
| 5 | 0101 | 1011 | 1000 | 0111 |
| 6 | 0110 | 1100 | 1001 | 0101 |
| 7 | 0111 | 1101 | 1010 | 0100 |
| 8 | 1000 | 1110 | 1011 | 1100 |
| 9 | 1001 | 1111 | 1100 | 1101 |
Todos esos códigos parten de la representación del bit, como una unidad mínima de información. Los números se agrupan en grupos de 4 bits formándo el byte, que son unidades de información y que te pueden empezar a sonar porque se utiliza en informática y programación.
En electrónica digital, se agrupan las diferentes codificaciones agrupan los números en bytes, por lo que el número final se compondrá de tantos bites como espacios ocupen. Así la primera decena de números decimales se podrán expresar con un byte (del número 0 al 9 en decimal). Pero a partir de la segunda decena hasta la primera centena (del número 10 al 99), se representará con dos bytes, y así sucesivamente se irá incrementándo el número de bytes de acuerdo al valor del número decimal traducido.
El número 9(10) (a partir de ahora utilizaré una notación de subíndices para indicar la base), en binario es 1001 según la codificación BCD. Pero si calculamos el número 99(10), verás que forma dos byte y el número 1100011(2). Observa que le falta un número al sistema del segundo byte. Ese es el signo del número. Como no tiene signo, se queda la representación tal cual puedes ver.
Por notación se toma que para un número positivo (+), se tiene que añadir al inicio del grupo de byte un cero. Y si el número es negativo se añade un uno. Asi el anterior número 99(10) = 01100011(2), indicándo que el número es positivo (aunque la primera forma sin el cero inicial también está bien expresada).
Así podemos deducir que el número absoluto de 99(10) es 1100011(2), pero el número con magnitud y signo es 01100011(2)
Más adelante volveremos con esto.
Algebra de Boole.
El algebra de Boole fue desarrollada en el siglo XIX por George Boole. Dicha algebra se basa en la naturaleza binaria de sus elementos que pueden adoptar el valor de cero y uno relacionando dichos elementos en operaciones básicas como la suma lógica, el producto lógico y la negación.
La relación de variables lógicas con las operaciones del ágebra de Boole reciben el nombre de función lógica o función booleana y se utilizan en electrónica digital para representar el estado que adoptará la salida o salidas de un circuito digital dependiendo del estado de sus entradas.
Para representar numericamente una función se emplea el uso de tablas de verdad, que indica el valor lógico que adoptará el valor lógico que adoptará la salida para cada combinación de las variables de entrada.
Por lo tanto, las tablas de verdad tienen tantas columnas como variables de entrada y salida tenga la función y tantas filas como sean posibles combinaciones que puedan darse con las variables de entrada.
Postulados.Son los siguiente:
● A + 1 = 1: La suma de una variable más uno es igual a uno.
● A + 0 = A: La suma de una variable más cero es igual a esa variable.
● A x 1 = A: El producto de una variable por uno es igual a esa variable.
● A x 0 = 0: El producto de una variable por cero es igual a cero
● A + A = A: La suma de una variable por ella misma es la propia variable.
● A x A = A: El producto de una variable por si misma es dicha variable.
● A + ¬A = 1: La suma de una variable con su negación es 1.
● A x ¬A = 0: El producto de una variable con su negación es cero.
● ¬¬A = A: Una variable dos veces negada es el valor de la variable.
Propiedades.
Álgebra de Boole se basa en las propiedades siguientes:
● Conmutativa: A + B = B + A y A x B = B x A
● Asociativa: A + B + C = A + (B + C) y A x B x C = A x (B x C)
● distributiva: A x (B + C) = A x B + A x C y A + (B x C) = (A + B) x (A x C)
Teoremas.
Los teoremas de dicho álgebra son:
● Ley de absorción: A + (A x B) = A y A x (A + B) = A
● Ley de Morgan: ¬A + ¬B = ¬A x ¬B y ¬ A x ¬B = ¬A + ¬B
NOTA: El signo ¬ significa negación, es decir el símbolo inverso. Por ejemplo la negación de A es ¬A (si A vale 1, ¬A vale 0).
Operadores lógicos.
Para el diseño de circuitos lógicos se emplean circuitos electrónicos construidos a partir de componentes como transistores, resistencias y diodos que reciben el nombre de puertas lógicas y representan los operadores lógicos del álgebra de Boole.
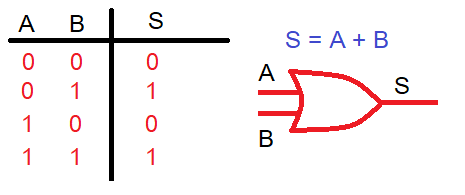
Función OR:Realiza la suma lógica de las variables de entrada:
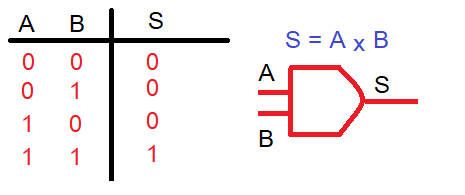
Función AND:Realiza el producto lógico de las variables de entrada.
Función Inversora:Realiza la negación de entrada.
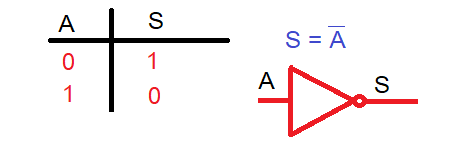
Si la función inversora se aplica a los tres resultados anteriores obtenemos nuevas funciones.
Función NOR:Realiza la suma lógica de las variables de entrada pero negándo la salida.
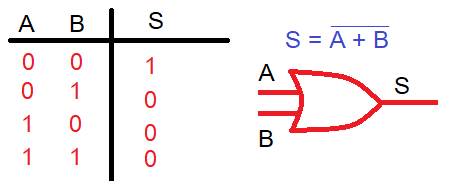
Función NAND:Realiza el producto lógico de las variables de entrada pero negando la salida.
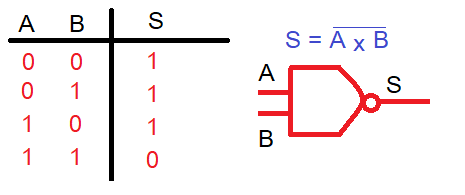
Función Buffer:Toma la salida el mismo valor que entrada. Se utiliza como amplificador de corriente.
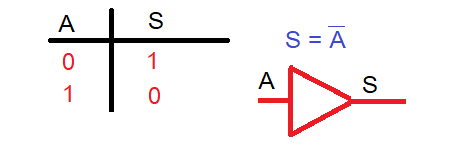
Además podemos definir dos nuevas funciones:
Función EXOR u OR exclusiva:La salida toma el valor de 1 cuando una y solo una de las entradas tengan dicho valor.
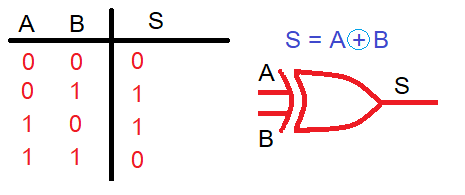
Función EXNOR u NOR exclusiva:Realiza la función anterior pero invirtiendo el resultado.
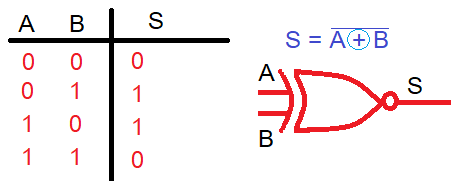
Podemos desarrollar un circuito digital, a partir de la función lógica, utilizando los operadores necesarios.
En el siguiente circuito se desarrolla la función S = A x B + A x ¬C.
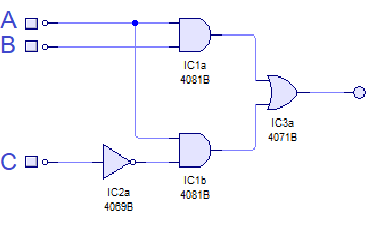
A los operadores del tipo NOR y NAND se les conocen como operadores universales puesto que con ellos podemos desarrollar cualquier función. Con estas puertas podemos implementar el resto de funciones OR, AND, Inversión, NOR, NAND, Buffer, EXOR y EXNOR.
Simplificación de funciones.
Si quieres diseñar un circuito combinacional es conveniente comenzar por elaborar una tabla de verdad, donde se indicarán todas las posibles funciones combinacionales que puede adquirir una entrada y su valor que puede tomar a la salida. A partir de la tabla, se obtendrán las ecuaciones del circuito.
Los valores que pueden obtenerse en forma de suma de productos, Miniterminos o Minterm; o en forma de productos de suma, Máximotérminos o Maxterm.
Para obtener la ecuación en Minterm, se toman todas las combinaciones de la tabla de la verdad en las que la salida adopta un valor de lógico de 1 relacionadas mediante sumas lógicas. Cada una de estas operaciones generará un minitérmino en el que aparecerá las variables de entrada relacionadas mediante productos lógicos. Si la variable toma el valor de 1, en dicha combinación aparecerá de forma directa, y si toma el valor cero, aparecerá de forma negada.
La ecuación de Maxterm se obtiene tomando las combinaciones de la tabla de la verdad en las que la salida adoptará el valor lógico 0, relacionadas mediantes productos lógicos. Cada combinación originará un Maxterm en el que aparecerán las variables de entrada relacionadas por las sumas lógicas. Si la variable toma el valor 0, aparecerá de forma directa, y si toma el valor 1 aparecerá negada, al contrario de lo que ocurría en los Minterm.
Una tabla de verdad puede construirse dependiendo de los resultados lógicos. Por lo que en la siguiente práctica veremos casos de usos y ejercicios para entender la tabla de verdad.