CIRCUITOS RESONANTES. SINTONIZACIÓN.

Se ha visto que la reactancia inductiva X_l, y la reactancia capacitiva X_c, están desfasadas entre sí 180º. En la representación vectorial, ambas magnitudes están oposición de fase, por lo tanto la reactancia resultante será la diferencia entre ellas, quedando con la característica de la resultante:

Si X_l es mayor que X_c, la reactancia resultante tiene características inductivas. Si es mayor la reactancia capacitiva, la resultante será capacitiva.

Como X_l, aumenta su valor al aumentar la frecuencia y X_c disminuye su valor cuando, también aumenta la frecuencia, tiene que haber un valor de frecuencia en que ambas reactancias son iguales y de signo opuesto, por lo tanto se anulan entre sí quedando en el circuito la resistencia eléctrica como única resistencia. Al anularse las reactancias, el valor de la impedancia toma el valor de la resistencia eléctrica.

Esta condición es muy importante, se la denomina Resonancia y a la frecuencia que la produce se la denomina frecuencia de resonancia. Los circuitos que tienen elementos conectados en serie se les dice circuitos resonantes serie, y los circuitos que están conectados sus elementos en paralelo, se dice circuitos anti resonantes o circuitos resonantes paralelos.

Frecuencia de resonancia.

Existe una sola frecuencia, para un determinado condensador e inductor, que haga que las reactancias de ambos sean exactamente igual. Para esa misma frecuencia de resonancia, el comportamiento del circuito resonante y el anti resonante es completamente distinta.

La frecuencia de resonancia se puede determinar fácilmente:

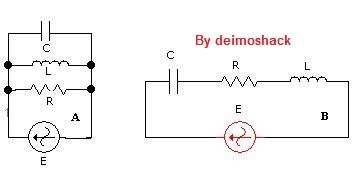
La gráfica siguiente muestra las curvas del condensador y de la inductancia en función de la frecuencia. Se da en el punto f₀, la condición de resonancia, ya que en este punto X_l = X_c. El valor de f₀ es la frecuencia de resonancia.

Este gráfico también te muestra unas condiciones de los circuitos resonantes:

A la frecuencia de resonancia:

Ofrecen una impedancia mínima, al tener valores resistivos únicamente y no introduce desfase.

Por debajo de la frecuencia de resonanacia:

Se tiene un valor de impedancia mayor que el mínimo y se comporta con características capacitivas, como si el circuito no tuviese inductancia provocando un adelanto de la intensidad.

Por encima de la frecuencia de resonancia:

Se tiene características inductivas y la intensidad se atrasa respecto a la tensión.

La frecuencia de resonancia se calcula con la fórmula matemática siguiente:

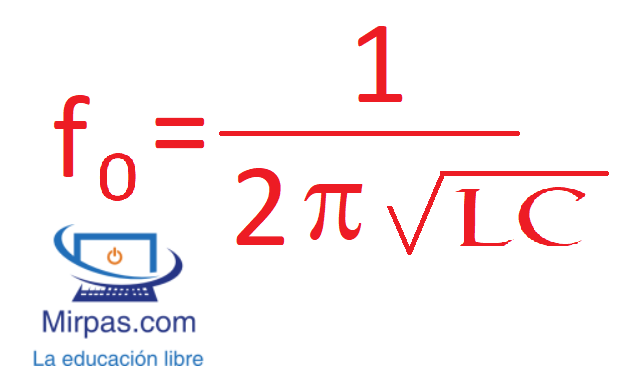
Siendo L en Henrios y C en Faradios.
Para que comprendas de donde viene esta fórmula, vamos a deducir dicha ecuación tomando la igualdad de las dos reactancias X_l = X_c.

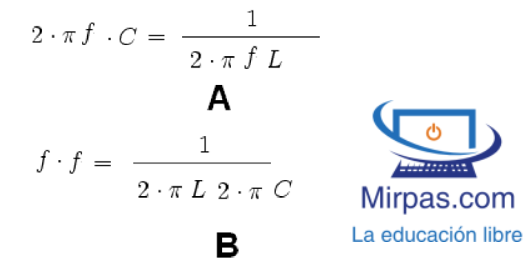
En A, hemos igualado las reactancias a 2 miembros.
En B despejamos la frecuencia y el primer termino de A pasa a B dividiendo. Agrupando términos semejantes:

Extraemos la raíz cuadrada en ambos términos y nos queda la formula final de la frecuencia de resonancia.
Luego también puedes calcular la capacidad y la inductancia, derivando la formula inicial. Te queda así:

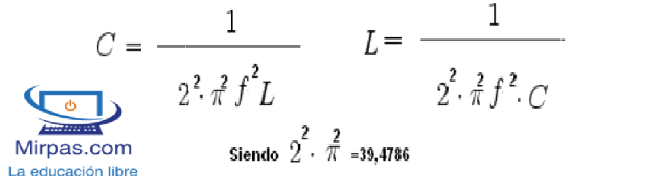
Este pequeño estudio sobre circuitos resonantes, te indica las características importantes que poseen los mismos, ya que a través de su frecuencia de resonancia y el cálculo de elementos, veras como se pueden obtener distintos valore de la F_o por lo que te permite realizar circuitos selectores de frecuencia. Este es el principio físico que utilizan los amplificadores sintonizados, los receptores de audio y video, osciladores y cientos de circuitos electrónicos que estudiarás en electrónica.

Circuitos resonantes serie

Se dice que un circuito es resonante serie cuando los tres elementos están conectados uno tras otro. Si este circuito se conecta a C.C, no ocurre nada especial, circula corriente durante un instante y luego se detiene la corriente al cargarse el condensador.

Pero si lo conectamos a C.A., cambia su comportamiento, presentando varias características importantes.

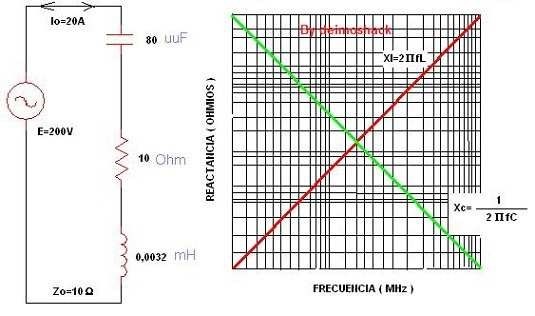
El circuito de la figura, está en resonancia a la frecuencia aproximada de 10MHz (unos 10.000.000 Hz). En la gráfica ves, a escala logarítmica, el punto en el cual las reactancias tienen un valor similar. El valor para esta frecuencia será de:

Y va a circular una corriente de:

La impedancia que ofrece la corriente, es del mismo valor que la resistencia óhmica, ya que las reactancias son del mismo valor y se anulan por ser opuestas quedando el circuito sin reactancia, pero no significa que no hayan desaparecido como tal, en forma individual está presente en el circuito y actúan, como tal. La corriente es de 20 A. Como se calculado aplicando la ley de Ohm y al atravesar la resistencia óhmica, desarrolla una diferencia de potencial de:

Pero esa misma corriente atraviesa la inductancia y también va a desarrollar un diferencia de tensión en ella:

En el condensador ocurre lo mismo, lo que ocurre que el valor es contrario al que se obtiene de la inducción, por tanto se anulan dichas tensiones en el circuito, dejando como resultante la diferencia de potencial desarrollada en la resistencia.
Es posible que te llame la atención el valor de la caída de tensión del inductor y del condensador. Esto se debe en parte a que la reactancia de ambos elementos es superior a la de la resistencia, pero en el circuito desaparece por la anulación mutua de reactancias.

Otra cosa: verás que se cumple que las sumas de las caídas de tensión parciales a lo largo de un circuito es igual a la tensión aplicada al mismo.
Suma todos los valores:

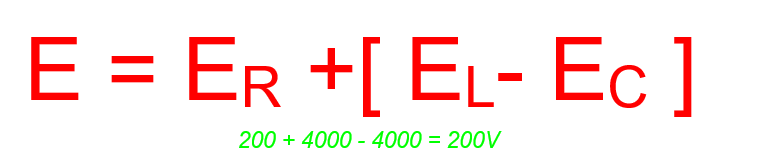
Factor Q:

Ahora bien, la relación en caída de tensión en la reactancia X_l y la tensión aplicada se llama ganancia de tensión.

Lo mismo sucede con el condensador, su reactancia es del mismo valor por estar en resonancia y la diferencia de potencial desarrollada tiene la misma magnitud, con signo opuesto. Si se mide con un voltímetro que no tenga consumo propio, entre los terminales A-B y B-C, se obtendrá una lectura de valor 4000 voltios, pero si la medición se hace desde A-C la indicación será cero.

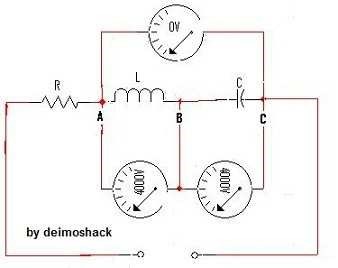
El hecho de que el condensador desarrolle elevada d.d.p. obliga a tener en cuenta que el dieléctrico del condensador sea capaz de soportar dicha tensión. No sirve de nada pensar que si la fuente aplica 200V y el dieléctrico soporta 600V el aislamiento es suficiente. Las condiciones siempre cambian al trabajar a la frecuencia de resonancia.

En el inductor no se presenta ese problema en forma tan notoria, porque la resistencia óhmica que se señala en el circuito, generalmente es la que corresponde al alambre de la bobina y por lo tanto, haciendo el triángulo vectorial de la d.d.p. en la resistencia y en X_l, da un valor de tensión que no presenta problemas.

Volviendo a la relación Q, del circuito resonante, que es el número que indica la cantidad de veces que aumenta la tensión reactiva E_l con respecto a la aplicada E. Analizando la ecuación se ve que si aumenta R, disminuye la ganancia Q del circuito, y por lo tanto la d.d.p. en X_l.

Este factor Q también se aplica a los inductores en forma aislada, considerando su relación entre su reactancia y su resistencia óhmica.

Curvas en el circuito resonante.

Como has aprendido, al valor de la frecuencia de resonancia, la impedancia es mínima.

Pero también hay una curva que permite establecer ciertas relaciones y poder hacer comparaciones con circuitos resonantes. Se trata de la curva que representa el paso de la corriente a través de un circuito resonante, para distintas frecuencias.

La curva de impedancia muestra cómo va variando su valor en función de la frecuencia. Por lo tanto el paso de la corriente en un circuito resonante se produce en función de la impedancia.

Así a la frecuencia de resonancia f_o, hay máxima intensidad y mínima impedancia (tal como muestran las gráficas).

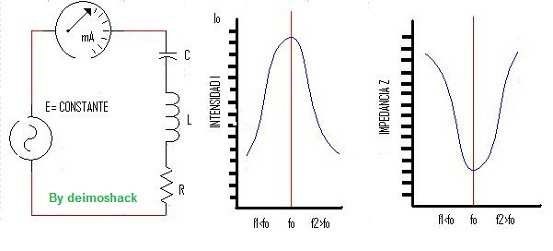
Esto solo se aplica a circuitos resonantes serie.

Prácticamente, la curva de la intensidad que circula por el mencionado circuito, es la misma que la impedancia, pero dada la vuelta que representa la curva de resonancia del circuito.
Se ve que a la frecuencia de resonancia, corresponde la máxima intensidad y que para cualquier frecuencia mayor o menor, disminuye la corriente. Cuanto más se aleja de f_o, mas disminuye la corriente. Ahora hace falta marcar un nuevo parámetro: el ancho de banda.

El ancho de banda del circuito, es un rango de frecuencias entre dos frecuencias delimitadoras.

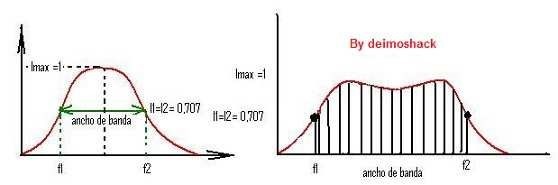
En la figura puedes ver una gráfica en la que se marca una frecuencia inferior f₁ (inferior a la frecuencia de resonancia f_o), y otra frecuencia f₂, superior.
Por tanto indicamos el ancho de banda como el intervalo de frecuencias entre f₁ y f₂.

Las frecuencias de f₁ y f₂ son las que producen menos trabajo en el circuito resonante, un trabajo en forma de potencia, cuyo valor sea la mitad de la máxima potencia disipada en el mismo. En el caso de la máxima disipación se produce con la frecuencia de resonancia. En las curvas que se representan a un circuito resonante serie, determinamos el valor de la corriente que corresponde a la mitad de potencia.

Un poco de matemáticas simples nos indica que es el 0,707 de la máxima corriente. Es decir un 70,7%. Veámoslo:

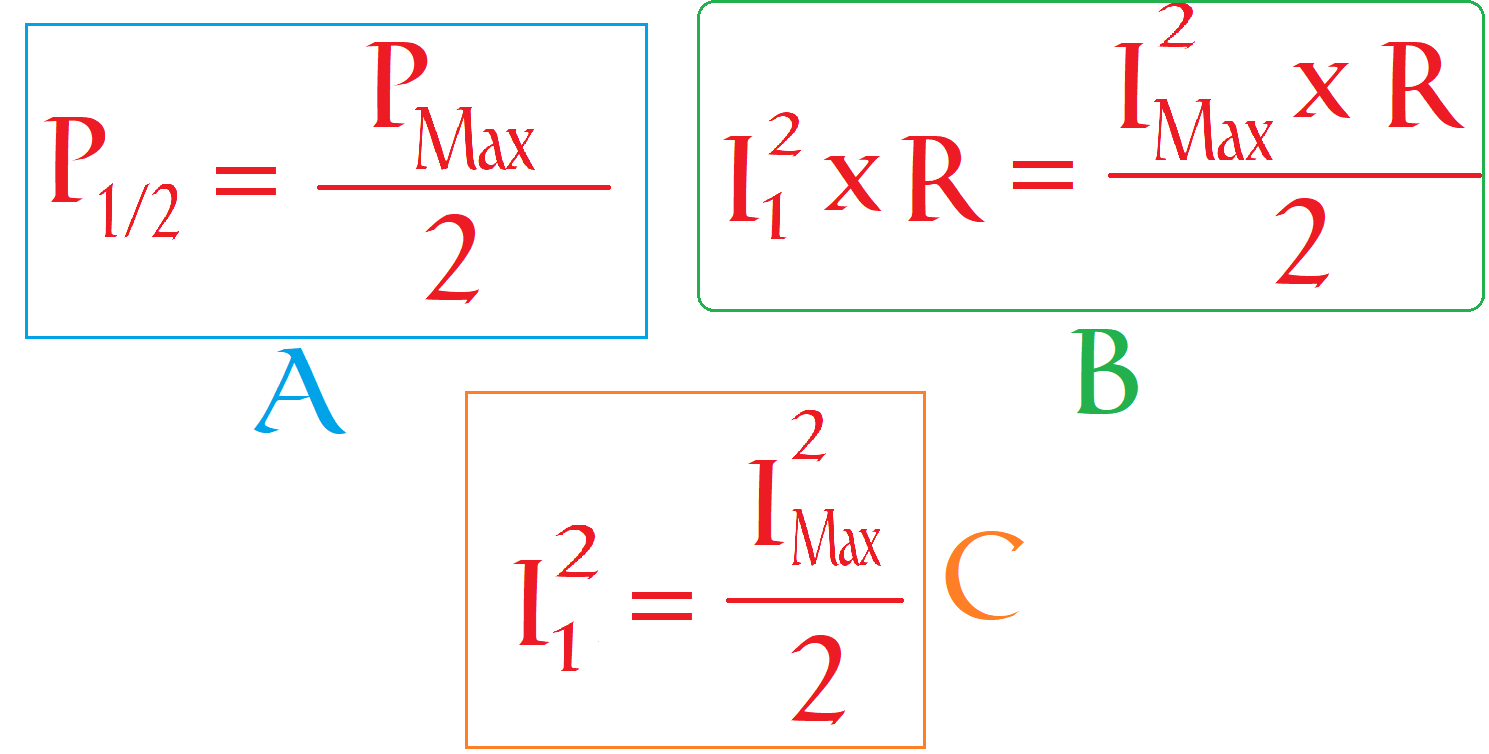
Reemplazamos ambas potencias por sus equivalente, I₂ x R, indicando con I₁ la corriente que corresponde a la potencia mitad y con I_Max la correspondiente a la máxima potencia, tenemos la formula (B). A ésta, eliminamos R, ya que está multiplicando en ambos miembros y nos queda (C). Y como los 2 miembros están al cuadrado, factorizamos con raíz y nos queda una solución de:

En las gráficas de arriba, las intensidades I₁ e I₂ corresponden a las frecuencias f₁ y f₂ y tienen una amplitud de 0,707 del máximo, al que en este caso, como ejemplo, le he dado un valor de 1 Amperio, por tanto a f₁ y f₂ les corresponde una corriente de 0,707A e indican las frecuencias límites que señalan el ancho de banda.

Selectividad

Los circuitos resonantes (sintonizados), nos permiten seleccionar la frecuencia correspondiente a una emisora o canal de televisión o radio. Pero tienen que tener la capacidad de separar las distintas estaciones sin que se lleguen a mezclar. Esta cualidad, la de poder separar las frecuencias unas de otras, se denomina selectividad.

El ancho de banda tiene mucha importancia, ya que un circuito con ancho de banda grande, deja pasar un amplio rango de frecuencias y pueden pasar 2 frecuencias que necesitan ser separadas. Sin embargo, si el circuito dispone de un ancho de banda reducido, resulta fácil separar las frecuencias, impidiendo que se puedan mezclar.

En la figura siguiente, se observa el gráfico de las frecuencias de 600Khz, la de 1000Khz y la de 1200Khz. Estas frecuencias pasan sin dificultad, ya que el ancho de banda es amplio; pero en el gráfico de al lado (B), se muestra un ancho de banda muy reducido, y como se ve, la frecuencia de 1000Khz pasa perfectamente, pero las de 600Khz y las de 1200Khz no pueden pasar.

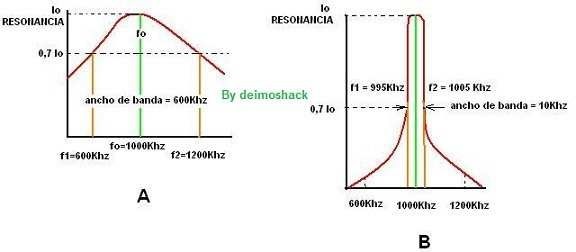
La curva de resonancia de la gráfica B, es más aguda y tiene mayor selectividad que la de la gráfica A.

Los circuitos más selectivos o agudos desarrollan a la frecuencia de resonancia, una señal de mayor amplitud que en los circuitos menos selectivos. Nos indican que, a la frecuencia de resonancia, la misma en ambos circuitos, la corriente que circula es menor en el circuito de mayor ancho de banda que en el de menor ancho de banda. Como a esa frecuencia, lo único que limita el paso de la corriente es la resistencia óhmica, quiere decir que dicha resistencia es de mayor valor en el circuito de mayor ancho de banda y menor en el más agudo. Como has estudiado también el factor Q o de sobre tensión; en el caso de la selectividad, Q interviene, ya que es la relación X_l÷R, cuanto mayor es R menor es Q. Por tanto un circuito muy agudo tiene un alto Q; un circuito con bajo Q significa que a la frecuencia de resonancia desarrolla una señal de menor amplitud y tiene un ancho de banda mayor.

Circuito antirresonante o resonante paralelo.

Este circuito, como su nombre indica, tiene los elementos L y C conectados en paralelo. La resistencia se coloca en la rama de la inductancia. Al igual que el circuito serie, el valor de la frecuencia de resonancia se calcula de la misma manera:

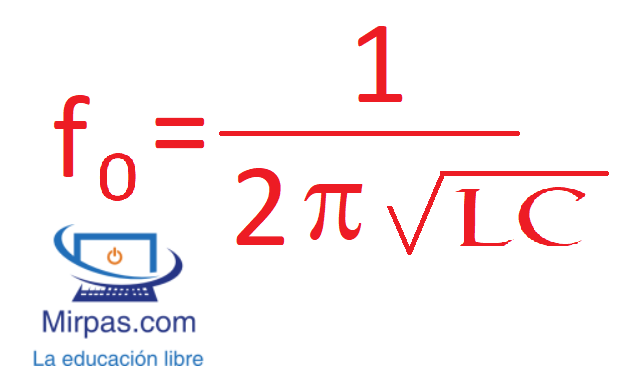
Pero sus características son totalmente diferentes. Voy a comparar las características del circuito resonante:

A la frecuencia de resonancia, el circuito paralelo ofrece máxima impedancia y en serie, mínima.

A la frecuencia menor a la de resonancia, el circuito paralelo actúa como una impedancia, y la serie como un condensador.

A la frecuencia mayor a la frecuencia de resonancia, el circuito anti resonante actúa como un condensador, mientras que en el circuito serie, actúa como una inductancia.

A la frecuencia de resonancia, ambos circuitos actúan como resistencias óhmicas, cuyo valor en paralelo, es máximo y en serie, es mínimo.

A la frecuencia de resonancia, con el agregado de una resistencia en cualquier de sus 2 ramas del paralelo, la impedancia disminuye, y en el circuito serie, si se le agrega una resistencia serie, aumenta la impedancia.

En el circuito serie, el parámetro de la corriente que se toma como referencia es la intensidad, cuyo valor es el mismo para todos los elementos conectados en serie. La tensión entre los bornes de cada uno de los elementos puede ser distinta, y su suma vectorial tiene que ser del mismo valor que la tensión aplicada al circuito. En el circuito paralelo, el parámetro que se toma como referencia es la tensión aplicada al circuito, ya que la intensidad por cada una de las ramas es independiente entre sí.

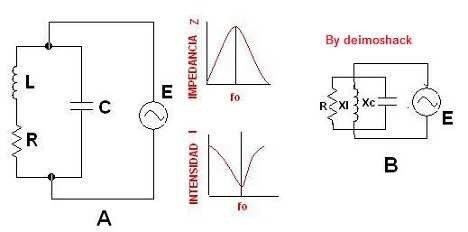
La variación de la intensidad de corriente y la impedancia de un circuito paralelo, se muestra en la gráfica de la derecha, donde observas que a la frecuencia de resonancia, se obtiene máxima impedancia Z y mínima intensidad I.

El valor de la impedancia se calcula con la ecuación que se deduce del circuito B:

La corriente total I_t es igual a la suma algebraica de las corrientes parciales I_R, I_LL e I_C. Si reemplazamos estas corrientes por sus equivalentes referidas a la tensión:

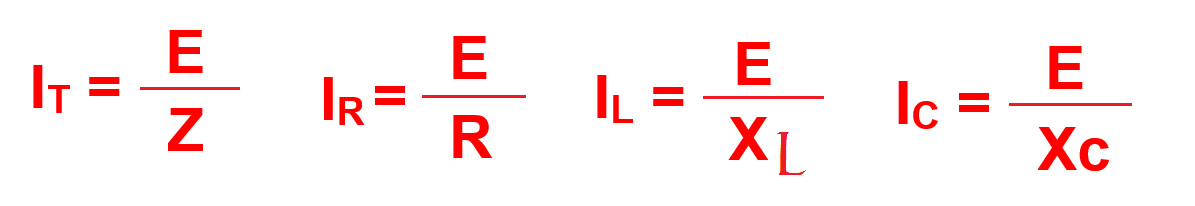
Dividimos las intensidades parciales:

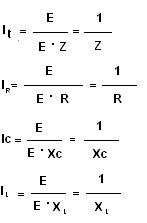
Pero si I_T es la suma geométrica de I_T, I_L e I_C, ( I_T ÷ E ), también será la suma geométrica de ( I_L ÷ E ), ( I_C ÷ E ) e ( I_R ÷ E ), es decir, para obtener el valor de ( 1 ÷ Z ) habrá que sumar geométricamente ( 1 ÷ R ), ( 1 ÷ X_L ) y ( 1 ÷ X_C ). La hipotenusa será la suma geográfica de ambos, es decir (1 ÷ Z). Aplicamos el teorema de Pitágoras:

Hipotenusa2 = (1ertermino)2 + (2ºtermino)2

Es conveniente que sepas que en los circuitos anti resonantes se puede operar también con las inversas. En el caso de las resistencias, eran las conductancias, que se representaba con la letra C (que es igual a 1÷R), las que se sumaban. En el caso de las reactancias en paralelo, se trabaja con las inversas de las mismas 1 ÷ X, tanto inductivas como capacitivas, que se llama Susceptancia y se simboliza por S.

Sumando la susceptancia y la conductancia del circuito, se obtiene la Admitancia representada por la letra Y y es la inversa de la impedancia Z.

Bien ya has terminado la parte teórica. Ahora visita el enlace de prácticas AQUÍ, para aumentar tus conocimientos.