Impedancias.
El estudio de vectores sirve para interpretar con claridad lo que sucede con el desfase, con la componente reactiva y la resistiva. Ayuda saber de vectores y trigonometría. Un vector es un segmento orientado que posee magnitud (parte designada del vector). Se llama módulo al valor del segmento. Tiene una dirección y un sentido.
En la imagen se muestra la componente vectorial del movimiento ascendente de las magnitudes de tensión y corriente desfasadas unas de otras (reactancia capacitiva en este caso).
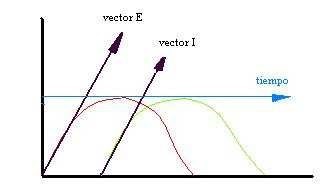
Observa que los vectores E e I tienen un origen, una dirección y un sentido.
Suma de dos vectores.
En el caso particular de nuestro estudio, los vectores tienen un único punto de aplicación, lo que simplifica el operar con ellos.Queremos sumar los vectores del ejemplo anterior. Para ello utilizaremos el método más sencillo; el método del paralelogramo.
Se cogen los vectores E, I y se pone uno de ellos en la misma dirección y sentido que en la gráfica anterior. El otro se pone en el mismo sentido, pero su dirección está desplazada para formar un ángulo de 90º con respecto al primero (tangencialmente). Esto generará un paralelogramo que, uniendo la punta de los vectores (vértices), nos dará el vector suma de E+I al que se la llama Resultante.
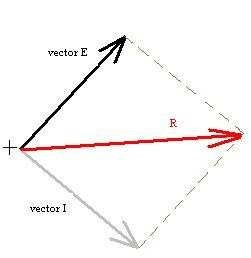
Otro método para calcular la resultante es la de coger los vectores en su dirección y sentido y ponerlos uno a continuación de otro. Esto es una suma directa y la resultante es igual. Este último método se utiliza para calcular la suma de sus módulos (partes en que está dividido un vector).
Resta de un vector
Para la sustracción debemos de cambiar el sentido de uno de los vectores y actuamos haciendo una suma directa. Es decir, si el vector I lo unimos al vector E, pero de sentido contrario (la flecha mirando al contrario), a lo mejor el vector I no ocupa toda la totalidad del vector E, y a lo que quede del vector E, se le dice Resultante de la sustracción. Puede ocurrir que la resultante sea del vector I; en este caso se considera resultante negativa.
Impedancia.
Ya conoces la reactancia y la resistencia eléctrica.
En C.A. la combinación de inductancia, capacidad y resistencia da por resultado una impedancia. La impedancia establece un nuevo valor de la resistencia aparente que se opone al paso de la corriente eléctrica con su característica de atrasar o adelantar la corriente o no modificar ese desfase. La impedancia se representa por la letra Z.
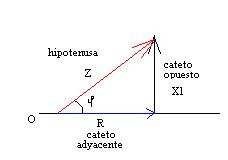
Para obtener la impedancia recurrimos al triángulo vectorial, colocando en el eje de referencia OX el valor de la resistencia, a 90º positivos, desde el punto de vista A, el vector de la reactancia inductiva, y negativamente el vector de la reactancia capacitiva.
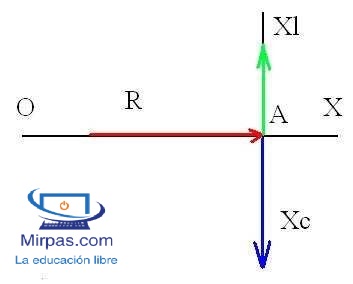
Se pueden representar 3 casos de impedancia:
Caso a:
Cuando un circuito está formado por resistencia y reactancia inductiva se calcula la impedancia con el triángulo vectorial. Se aplica el teorema de Pitágoras que dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos; es decir es lo mismo que:
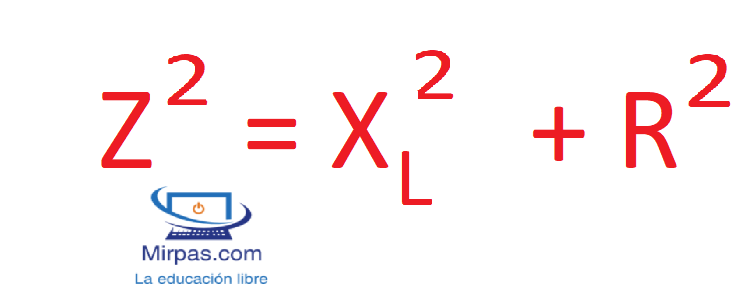
Caso b:
Si el circuito tiene Resistencia y reactancia capacitiva, se procede de la misma manera, pero teniendo cuidado de colocar la posición del vector de capacidad opuesto al vector inductivo (hacia abajo). Pero la resolución es la misma:
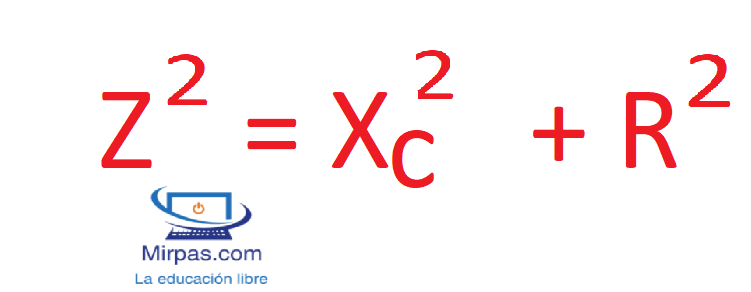
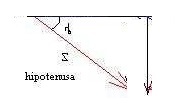
Caso c:
En un circuito donde hay conectado en serie una resistencia, una inductancia y un condensador, se calcula el valor de la impedancia igual que en los casos anteriores, teniendo en cuenta que la reactancia inductiva y la reactancia capacitiva se oponen en su comportamiento. Se pueden presentar 2 casos: que la inductiva sea mayor que la capacitiva o, a la inversa, que la capacitiva sea superior que la inductiva. Matemáticamente se calcula la reactancia total de ambas y se suma la resistencia eléctrica.
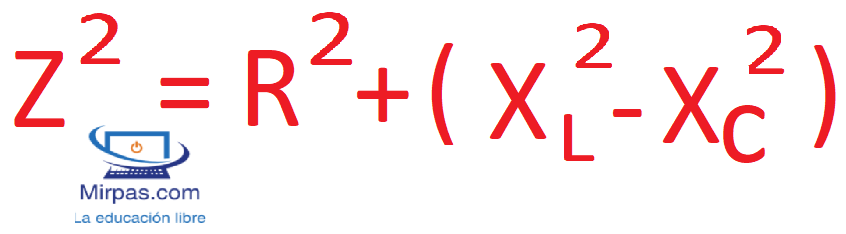
Susceptancia y admitancia.
En el tema 3 vimos los efectos de la resistencia que, al agruparse en los circuitos con otras resistencias en paralelo, disminuía la resistencia total; es decir aumentaba la conductividad en el circuito. En realidad la conductancia es la inversa de la resistencia. Lo mismo sucede en los elementos reactivos cuando se conectan varios en paralelo, que hay que realizar cálculos, así pues la inversa de la reactancia es la susceptancia.
Esta magnitud se mide en Mohm (Ohmios reactivos a la inversa) y se representa con el símbolo S con el subíndice correspondiente si es inductivo o capacitivo.

La admitancia es la inversa de la impedancia, al igual que la susceptancia es la inversa de la reactancia y la conductividad es la inversa de la resistencia. Se designa por la letra Y y no existe en este caso subíndice. Se mide en Mohm y su expresión matemática es:
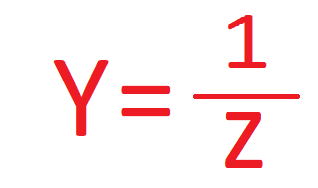
Circuitos en serie en C.A.
El circuito siguiente te muestra un circuito serie con resistencia, inductancia y capacidad.
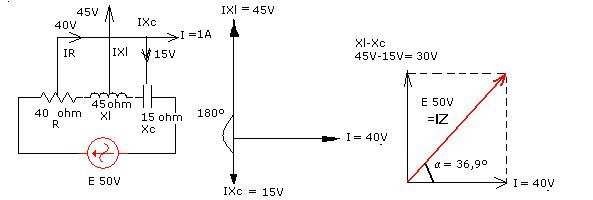
La corriente i constituye la referencia común en cuanto a las caídas de tensión en los 3 elementos, puesto que la intensidad es la misma en los 3 componentes (componentes en serie). Esta referencia está indicada por la línea horizontal sobre la que se encuentra el vector correspondiente a la caída de tensión sobre la resistencia en el circuito de la izquierda.
El vector representativo de la tensión en cada elemento, mostrando la relación de fase, con respecto a la corriente común (línea horizontal), lo puedes ver trazado justo encima de cada elemento, mostrando la relación de fase con respecto a la corriente común.
La suma vectorial de las tres caídas de tensión IR, IXl e IXc debe ser igual a la tensión total aplicada E al circuito.
Los 3 vectores trazados a escala (figura central), se disponen a la suma vectorial. Puesto que las tensiones IXl e IXc están respectivamente opuestas y desfasadas entre sí 90º con respecto a IR, y 180º entre ellas, la suma vectorial Xl - Xc es sencilla.
En el dibujo de la derecha se observa la suma vectorial ya realizada la suma vectorial de los componentes Xl y Xc y sumado al valor R. De aquí deducimos el valor de la impedancia total Z.
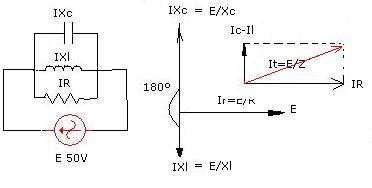
Circuitos en paralelo en C.A.
En este caso se sigue el procedimiento vectorial, pero actuamos con las corrientes en vez de con las tensiones. En la figura observas el circuito en paralelo, el desfase de reactancias y la suma vectorial. Observa que en el desfase, la reactancia capacitiva es superior a la inductiva. Esto se debe a que en un condensador la intensidad se adelanta con respecto a la tensión y en el inductor, se retrasa, lo que hace que ambas corrientes estén desfasadas 180º entre sí.
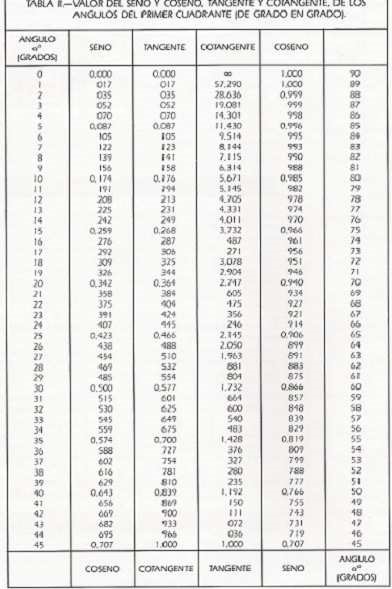
TAblas de conversión
Las tablas mencionadas en esta lección te va a resultar muy útil en el transcurso de este estudio ya que te indican las formulas para hallar Z y el ángulo de desfase en función de su tangente (tgα=senα ÷ cosα).
La tabla 2 es un extracto de las tablas trigonométricas donde están indicados los valores del seno, coseno, tangente y cotangente para los ángulos de 0º, 45º y de 45º a 90º.

Bueno, hasta aquí ha llegado el tema de las impedancias.
En próximos cursos verás que estos conocimientos que he expresado en el tema podrán ser aplicados sobre todo cuando estudiemos filtros y redes radioeléctricas.
Ahora visita el vídeo del tema para más información.
