EJERCICIOS RESUELTOS.
En esta clase nos vamos a centrar en la práctica de circuitos de álgebra de Boole para asentar más aún los conocimientos de ésta técnica.
En esta clase vamos a realizar una serie de ejercicios resueltos que sumados a los de la clase anterior serán suficientes como para poder pasar a nuevos contenidos. Espero que esta clase te permita adquirir los conocimientos necesarios sobre el álgebra de Boole.
Reducción de circuitos.Sea el siguiente circuito lógico:
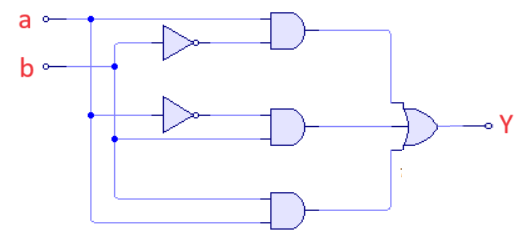
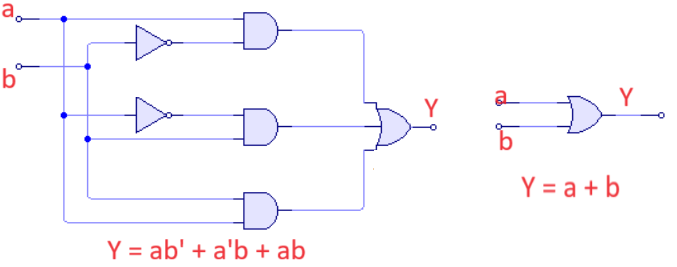
Reduce al máximo la ecuación siguiente:
Y = ab' + a'b + ab
Para empezar la recomendación a usar es Agrupar en términos pares, lo que implica buscar términos que sean comunes en dichas agrupaciones. Por ejemplo, en nuestra ecuación Y = ab' + a'b + ab, tenemos en común que de la última suma a'b + ab, la salida b es no negada en ambos términos, por lo que se puede sustituir de acuerdo a la siguiente ecuación:
Y = ab' + b(a'+a)
Esta acción se dice factorizar e implica agrupar términos comunes para poder reducir la ecuación según las leyes del álgebra de Boole.
De los prinicipios de dualidad de la clase anterior:

Sabemos que la suma de una puerta logica por su misma puerta lógica negada es igual a 1. Por lo tanto podemos sustituir nuestra ecuación como sigue (agrupando términos indenpendientes a la izquierda):
Y = b + ab'
Como puedes ver ahora podemos aplicar la propiedad distribuitiva A+(B x C) = (A+B)x(A+C), con lo que nos quedaría:
Y = (b + a)(b + b')
Fijate que en el segundo término obtenemos igual que al principio la suma de la puerta por su negada, por lo que nos da un 1, por lo que la función simplificada nos da una puerta OR habitual:
Y = a + b
Otra ecuación para aplicar la reducción es la siguiente:
Y=ab' + abc + ab'c + ab
Aunque parezca más dificil, no lo es porque tenemos términos que son iguales. Por ejemplo el primer término y el último comparten puertas (ab' y ab); mientras que el segundo término y el tercero también comparten puertas (abc y ab'c), por lo que podemos agrupar términos de la siguiente manera:
Y = ab' + ab + abc + ab'c
Como la entrada a en los dos primero términos anteriores es igual, aplicando al principio de dualidad nos queda que podemos multiplicar dicha puerta por las entradas b y b'. En los términos tercero y cuarto tenemos que las puertas comunes son la puerta a y la puerta c, por lo que en esta ecuación multiplicaremos dichas puertas por la suma de b más b', como ves continuación:
Y = a(b' + b) + ac(b + b')
Y ahora fijate que lo que queda en parámetro son sumas de puertas inversas, por lo que se puede sustituir por un 1 según el principio de dualidad. Entonces la ecuación simplificada sería:
Y = a + ac
Pero esto lo podemos seguir factorizando ya que como tenemos una misma puerta a, el resultado sería:
Y = a(1 + c)
Y teniendo en cuenta que según el principio de dualidad una puerta sumada a un uno, devuelve un 1, por lo que la ecuación final quedaría como:
Y = a
Otros ejercicios implica la operación de las puertas lógicas. Por ejemplo la ecuación:
(x + y)(x + z)
La operación es una operación de cada incógnita de cada término por la incógnita del otro término de la forma siguiente:
(xx) + (xz) + (xy) + (yz)
De los principios de dualidad recuerda que A * A = A, por lo que el primer término es igual a x. Eso nos deja la posibilidad de operar con el término inmediatamente superior:
x(1 + z) + xy + yz
Como uno más la letra es la unidad, la ecuación x(1 + z) quedaría como x(1), por lo que la ecuación tiene la forma hasta ahora:
x + xy + yz
Al igual que en la anterior operación, comparte la x en el primer y segundo término, por lo que podemos establecer que:
x(1 + y) + yz
Lo que nos queda una ecuación irreducible de:
x + yz
Ejercicios resueltos de Morgan.
El teoréma de Morgan nos decía que si una ecuación es negada, para resolverlo, hay que cambiar el tipo de operación e invertir el estado de las variables de la operación. Para ello vamos a ver una serie de ejercicios.
La siguiente expresión:
Y = (w + wx' + yz)'
Cambiamos el tipo de operación y negamos las entradas.
Y = (w' * (w' + x)* (y' + z') ))
Como puedes ver hemos hecho lo contrario a la ecuación original; las sumas se convierten en multiplicación y las variables se invierten en polaridad. Operando los términos quedan que:
Y = (w'w' + wx)(y' + z')
Como de la tabla de dualidad nos dice que una entrada por su misma entrada es la entrada, podemos establecer la operación del primer término como:
Y = w'(1+x)(y' + z')
Y como 1 más la variable siempre es 1, podemos reducir más aún la ecuación de la forma que nos queda una ecuación irreducible:
Y = w'(y' + z')
Dibujar diagrámas a partir de ecuaciones.
Otro de los ejercicios que nos suelen pedir a raíz de las ecuaciones es que dibujemos los circuitos o diagrámas esquemáticos del circuito lógico. La operación no conlleva mayor secretismo, pero simplemente debes de tener en cuenta que la operación de la puerta es una suma, la puerta será OR, mientras que si la operación es una multiplicación, será una puerta AND. La negada viene representada con un punto en la salida de cada puerta. El inversor es una puerta NOT. Así por ejemplo vamos a realizar los circuitos de las ecuaciones siguientes:
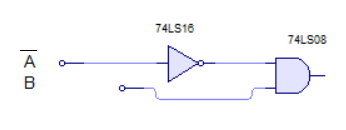
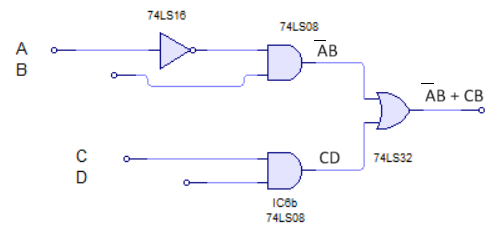
F = AB + CDLo que se recomienda es hacer poco a poco el diagrama según te encuentres el circuito. En el primer término tenemos que una entrada negada A que multiplica con una entrada B, por lo tanto es una puerta AND que en una entrada (A), tiene puesto un inversor como se vé en la siguiente imagen:
En la siguiente operación las entradas CD también están multiplicando, por lo que se aplica una puerta AND como verás en pantalla.
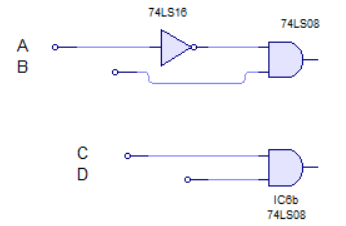
El resultado final lo obtenemos en el siguiente circuito.
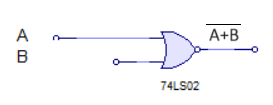
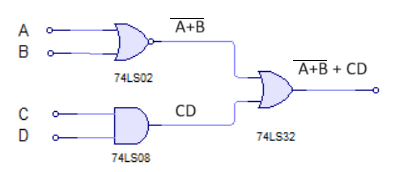
A+B + CDEn esta ecuación puedes ver que la entrada A+B es una puerta OR de tipo negado, mientras que se suma a una puerta AND no negada de la forma que la primera puerta OR negada es:
La puerta correspondiente a la entrada C y D es una puerta habitual AND, por lo que el resultado final de la ecuación es:
F = A + (CD)Este circuito es fácil teniendo en cuenta que la primera entrada se puede rerpresentar como una línea o un driver, mientras que las otras entradas están ligadas a una puerta AND. El resultado es el siguiente:
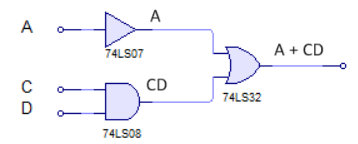
En la sección práctica veremos los integrados que forman las puertas lógicas AND, OR y NOT en específico.
Gracias por compartir el contenido en las redes sociales.