EXPRESIONES CANÓNICAS.

A la hora de diseñar un buen circuito digital combinacional, se empieza por elaborar la tabla de verdad, en donde se indicarán todas las posibles combinaciones de entrada y el valor que adoptará dicha salida. Es a partir de esa tabla cuando podemos empezar a desarrollar las ecuaciones del circuito.

Pero antes, repasemos cómo llegar a la tabla a partir de un circuito.

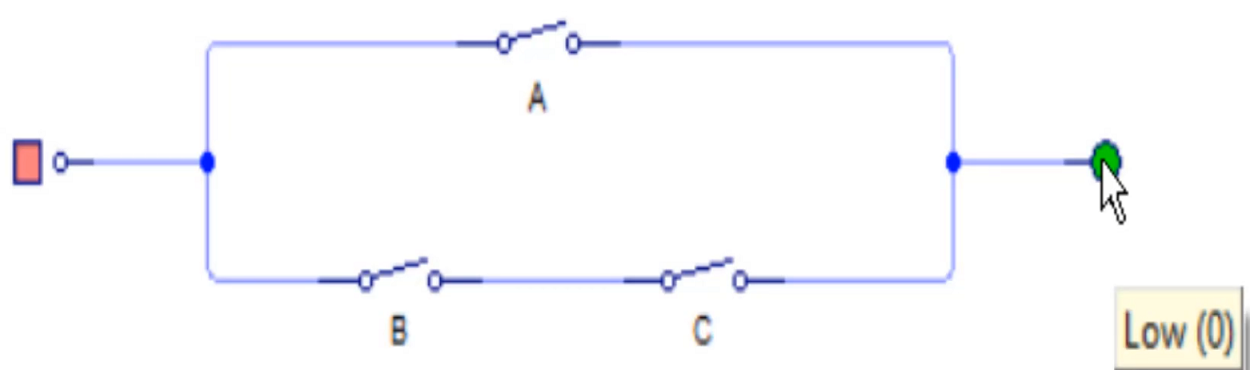
En el circuito anterior puedes un circuito paralelo en el que por la malla superior puedes ver un interruptor A; mientras por la otra rama un circuito serie con otros dos interruptores B y C. Dependiendo de la posición de las variables lógicas, se obtendrá una salida específica que podremos poner en la tabla de verdad.

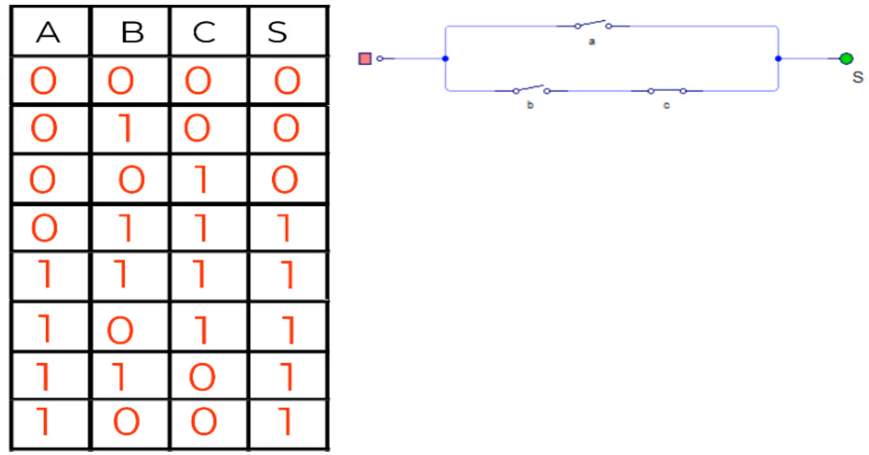
Si nos fijamos en el circuito, verás que cuando A está cerrado, existe un nivel lógico alto a la salida del mismo independientemente de como se encuentren las variables lógicas (los interruptores), de la rama serie, B y C. Y al revés, si A está abierto y en la rama inferior, se cierran B y C, también habrá una salida alta (solo en el caso de que ambos esten cerrados).

Podemos saber entonces que la ecuación que rigue este circuito es la siguiente:

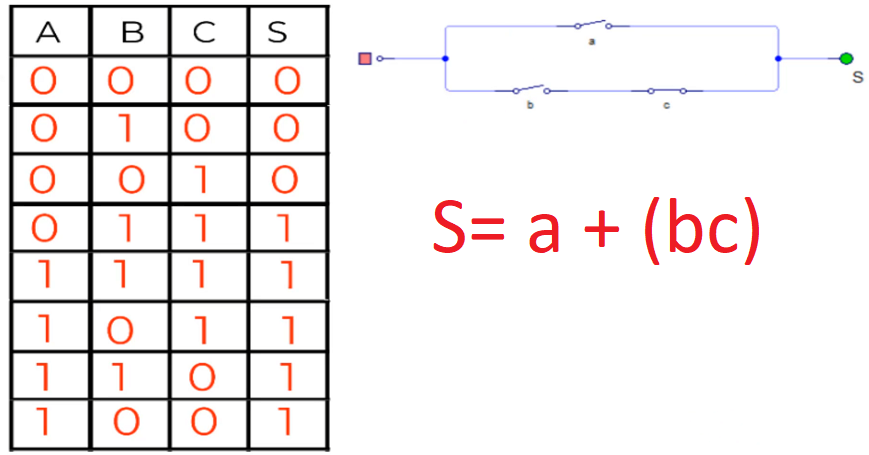
Recuerda que los circuitos en paralelo son lógica OR, porque mientras que una de las variables afectadas sea 1, la salida será 1 aunque el resto de variables sea 0. Mientras que los circuitos en serie son lógica AND y deben de estar en 1 todas las variables para que la salida sea 1.

Por eso a la hora de sacar la función del circuito tendremos en cuenta las variables del mismo, y la configuración de las mismas y, como vemos sabemos que la salida S viene dada por el estado de la variable A y el + indica que está en un circuito paralelo con la rama de las variables B y C, que están multiplicando (AND). Por eso, en esta ecuación lo más importante es el valor de A y que B y C sean 1.

Las diferentes posiciones de las variables lógicas producirán diferentes salidas que, como ves anteriormente he agrupado en orden ascendiente, viendo que solo hay tres salidas 0, en el circuito (para cuando A está abierta y B ó C ó ambas están abiertas. Y otras cinco salidas 1, cuando si conducen algunas de estas variables.

Para las salidas que devuelvan 0, puedo obtener un tipo de ecuación derivada de la principal que llamaremos maxterms o maxitérminos. Para las salidas que devuelvan 1, las llamaremos minterms o minitérminos. Tanto las ecuaciones maxterms como las minterms se llaman expresiones canónicas.

Maxterms.

Las ecuaciones maxterms o productos de sumas son todas las combinaciones de la tabla de verdad en la que la salida es 0. Y se relacionan entre ellas mediante productos lógicos. Cada combinación originará un maxterms en el que aparecerán las variables de entrada relacionadas por sumas lógicas.

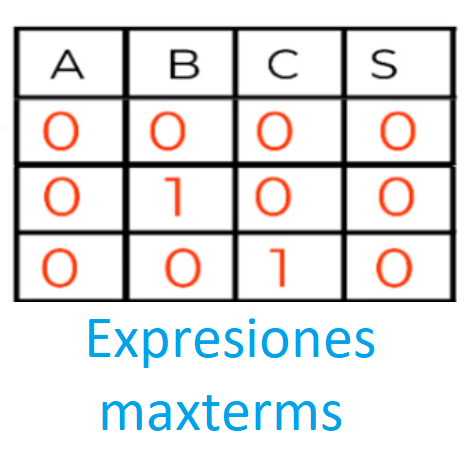
En la anterior imagen puedes ver cómo se muestran las variables de la tabla de verdad que dan como resultado el valor de 0 lógico. En esta situación, cuando la salida es cero la ecuación canónica es una maxterms, y tenemos que tener en cuenta el estado de cada variable binaria del circuito teniendo en cuenta esta regla:

● Si la variable lógica coincide con la salida, es decir 0, la variable será no negada.
● Si la variable es contraria a la salida, es decir 1, la variable será negada.

Entonces teniendo en cuenta esta regla podemos establecer que, para la primera fila:

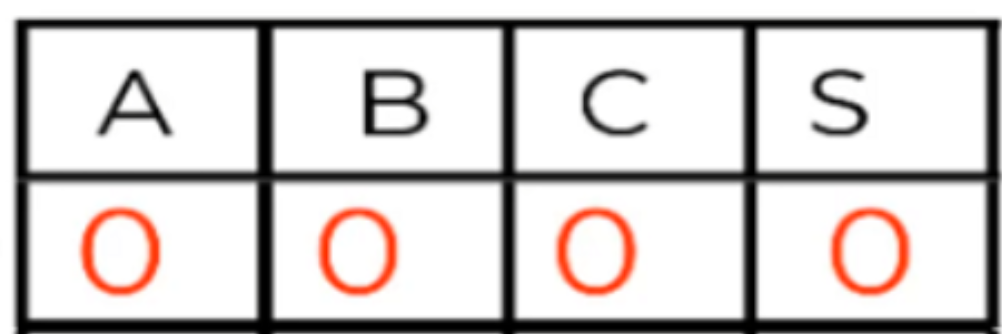
Para la variable A como el valor 0 coincide con la salida, esta variable es normal. Lo mismo podemos establecer para las variables B y C, por lo que queda que:

M0 = (A + B + C)

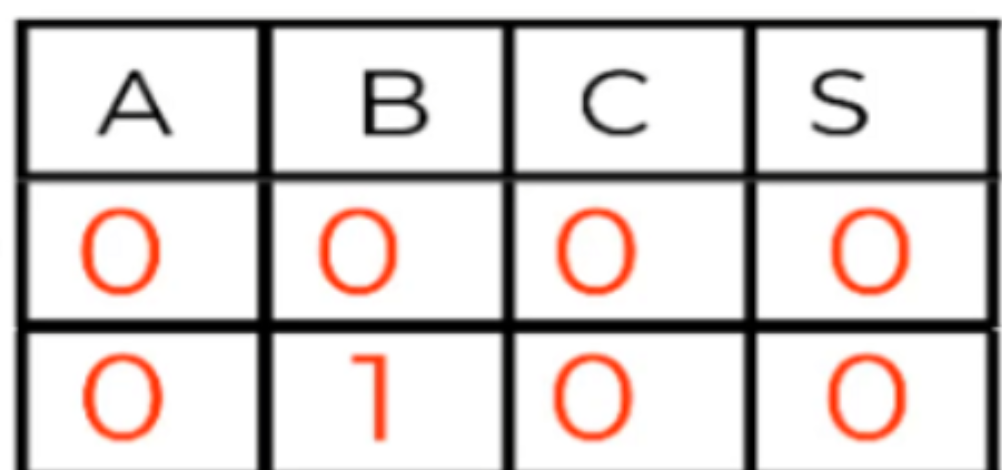
Para esta variable se repite la situación anterior, A es normal, pero la variable B es 1 por lo que entonces estará negada. C es normal también porque coincide con la salida.

M1 = (A + B + C)

Para esta variable tanto A como B son normales, pero la variable C es negada porque es contraria a la salida.

M2 = (A + B + C)

Las ecuaciones maxterms se representan mediante una numeración en mayúsculas. Y como son multiplicaciones de cada ecuación, la ecuación maxterms queda así:

S = M0 x M1 + M2

S = (A+B+C) x (A+B+C) x (A+B+C)

NOTA: las variables negadas se representan con una raya sobre su letra.

Minterms.

Las ecuaciones minterms o suma de productos son todas las combinaciones de la tabla de verdad en la que la salida es 1. Y se relacionan entre ellas mediante sumas lógicas. Cada combinación originará un minterms en el que aparecerán las variables de entrada relacionadas por productos lógicos.

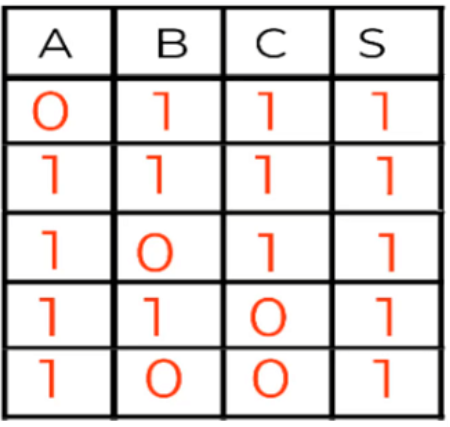
En la anterior imagen puedes ver cómo se muestran las variables de la tabla de verdad que dan como resultado el valor de 1 lógico. En esta situación, cuando la salida es uno la ecuación canónica es una minterms, y tenemos que tener en cuenta el estado de cada variable binaria del circuito teniendo en cuenta esta regla:

● Si la variable lógica coincide con la salida, es decir 1, la variable será no negada.
● Si la variable es contraria a la salida, es decir 0, la variable será negada.

Entonces teniendo en cuenta esta regla podemos establecer que, para la primera fila:

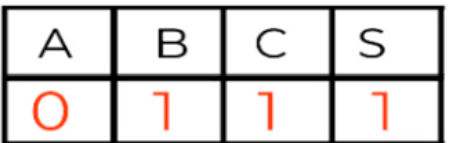
Para la variable A como el valor 0 no coincide con la salida, esta variable es negada. Mientras que las variables B y C, son normales:

m0 = (ABC)

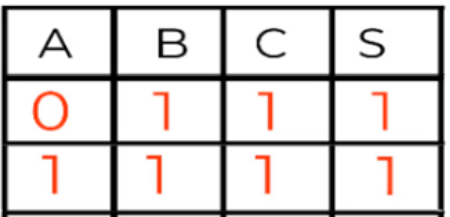
En esta fila todas las variables coinciden con la salida, por lo que su estado es normal.

m1 = (ABC)

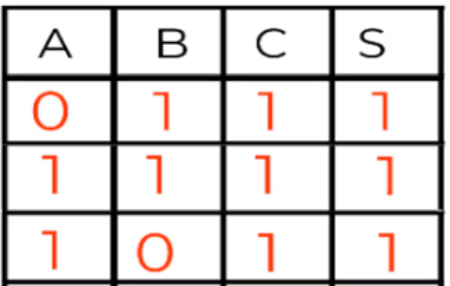
Para esta fila, la variable tanto A como C son normales, pero la variable B es negada porque es contraria a la salida.

m2 = (ABC)

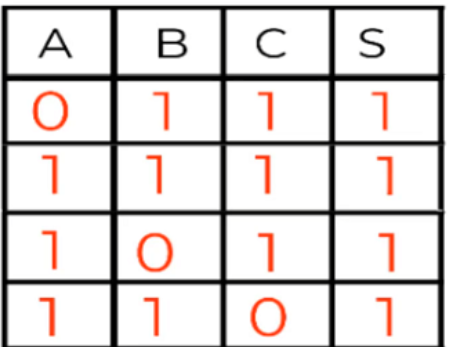
Para la siguiente fila (4ª), tenemos que:

m2 = (ABC)

Y para la última fila, la ecuación es:

m2 = (ABC)

Las minterms se representan mediante una letra minúscula y su subíndice de acuerdo a la posición en la que se encuentre la fila. Así podemos representar los minterms anteriores de la forma siguiente:

S = m0 + m1 + m2m3 + m4

S = (ABC) + (ABC) + (ABC) + (ABC) + (ABC)

Simplificando términos.

Si nos fijamos en las dos ecuaciones canónicas, podemos ver la diferencia entre ambas:

Sminterm = (ABC) + (ABC) + (ABC) + (ABC) + (ABC)

Smaxterm = (A+B+C) x (A+B+C) x (A+B+C)

Estas expresiones canónicas en su forma original son expresiones que podemos deducir para obtener la fórmula principal del circuito. Y dependiendo de la ecuación que uses (maxterms o minterms), el resultado será el mismo. Así que vamos a reducir las expresiones usando el álgebra de Boole.

Utilizaremos la siguiente tabla resumen donde están los tratados de dicha algebra, para poder reducirlos.

La acción de reducir significa convertir una expresión lógica a su mínima expresión representativa. Para ello vamos a empezar por la ecuación de minterms y nos ayudaremos del ágebra de Boole.

Reducir minterms.

Sminterm = (ABC) + (ABC) + (ABC) + (ABC) + (ABC)

Como son multiplicaciones, podemos coger los terminos que tengan variables comunes entre sí. Por ejemplo, veo que el segundo y cuarto término tienen variables comunes (AB resaltado en verde):

Sminterm = (ABC) + (ABC) + (ABC) + (ABC) + (ABC)

Y la C en la segunda variable es normal y en la cuarta variable es negada. Por lo tanto si operamos según el algebra normal podemos establecer que:

A(BC) + A(BC)

Como A multiplica a los dos terminos se puede sacar del segundo término:

A[(BC) + (BC)]

Y como B también es una variable que esté en ambos terminos, podemos seguir reduciendo:

A[B x (C + C)]

Lo cual nos queda que:

AB(C + C)

Y como la suma de una variable por su negada es 1, esta operación queda como:

(ABC) + (ABC) = AB

Ya hemos reducido dos terminos de la ecuación minterms. Vamos a ver qué más podemos reducir:

Sminterm = (ABC) + (ABC) + (ABC) + (ABC) + (ABC)

Del tercer y quinto conjunto, tenemos en común las variables A y B negada. Por lo que podemos reducirlas también de la forma parecida a la anterior:

AB (C + C)

(ABC) + (ABC) = AB

Y ya solo nos queda el primer término para reducir. Hasta ahora la ecuación minterms queda como se ve a continuación:

Sminterm = (ABC) + AB + AB

Por lo que podemos seguir reduciendo:

AB + AB = A (B + B) = A

Lo cual nos queda una ecuación de:

ABC + A

Si usamos la propiedad distributiva A + BC = (A + A) + (A +BC))

Nos queda entonces la ecuación irreducible siguiente:

Sminterm = A + BC

Calcular la ecuación maxterm.

La ecuación maxterm de esta tabla queda como ves a continuación:

Smaxterm = (A+B+C)M0(A+B+C)M1(A+B+C)M2

Para realizar la reducción de un sistema algebrico lógico siempre debes de fijarte qué variables son comunes en la ecuación para poder despejarlas mediantes las reglas del álgebra de Boole. Por ejemplo, si te fijas en la primera y el segundo término, puedes ver que los comunes son A y C, como resalto en verde:

Smaxterm = (A + B + C)M0(A+B+C)M1(A+B+C)M2

Entonces podemos agrupar de la siguiente manera:

(A + B + C)(A + B+ C) = [(A + C) + B][(A + C) + B]

Vamos a coger la variable (A + C), que coincide en ambos términos y la vamos a asignar a una letra PI mayúscula (Π) para poder operar con ella y así hacer una reducción según la propiedad distributiva.

Π = (A + C)

Entonces:

(Π + B)(Π + B) = (Π x Π) + (Π x B) + (B x Π) + (B x B)

Como Π por Π es la variable Π, y B por su negada es cero, la ecuación anterior queda así:

(Π + B)(Π + B) = Π + (Π x B) + (Π x B)

Y como Π está en todos los términos, se puede sacar de la siguiente forma:

Π (B + B)

Y como una variable más su negada es cero, la ecuación que queda es Π que es igual a A + C.

Ya nos queda realizar la ecuación (A + C)(A + B + C)M2. Multiplicamos las variables del primer término con las variables del segundo:

(A + C)(A + B + C)M2 = A ( A + B + C) + C (A + B + C)

AA + AB + AC + CA + BC + CC

Como una variable por sí misma es la variable, y una variable por su negada es cero, actualizamos:

A + AB + AC + CA + BC

Y como A se encuentra en los 4 primeros términos, podemos sacar A de los mismos:

A (1 + B + C + C) + BC

Y como 1 + B es 1 y C por su negada es cero, reduciendo nos queda que la ecuación maxterm es igual a:

Smaxterm = A + BC

Si te fijas en la solución de la ecuación minterm es la misma que la ecuación maxterm. Esto indica que se ha realizado correctamente el calculo de la ecuación canónica. Cada resultado indipendiente de las expresiones canónicas dan como resultado la función resultante del circuito lógico.

Gracias por compartir el contenido en las redes sociales.