MAPAS DE KARNAUGH PARA SIMPLIFICAR CIRCUITOS.

Como hemos visto anteriormente la reducción de las ecuaciones lógicas depende exclusivamente de los conocimientos del álgebra de Boole del usuario, y como la reducción máxima está ligada a la capacidad y conocimientos del técnico electrónico, es posible que se produzcan fallos o no se alcance a la máxima reducción del circuito.

Los mapas de Karnaugh es el método más extendido y es más fiable que la reducción mediante aplicación del álgebra de Boole, ya que no entra tanto en juego el cálculo aritmético sobre las variables lógicas. Los mapas de Karnaugh son un método gráfico, por lo que sus resultados son de fácil comprensión y se obtiene buenos resultados.

Pero hay reglas que hay que tener en cuenta:

● Se usan exclusivamente para simplificar circuitos.
● No utilizar para circuitos con más de 4 variables.

Con los mapas de Karnaugh vamos a hacer lo mismo que hemos hecho en la parte anterior teórica, pero de una manera visual por lo que se nos mostrará más sencillo y de una manera más rápida. No se suele utilizar en dos variables porque es demasiado simple y esas operaciones se suelen resolver mediante el álgebra boleano. Además, no se suelen utilizar más de 4 variables porque el mapa generado sería un intrincado demasiado complicado como para no liarse en la reducción del circuito (y se tendrían que usar otros métodos más avanzados para circuitos con más variables lógicas), como por ejemplo el de Quine-McCluskey.

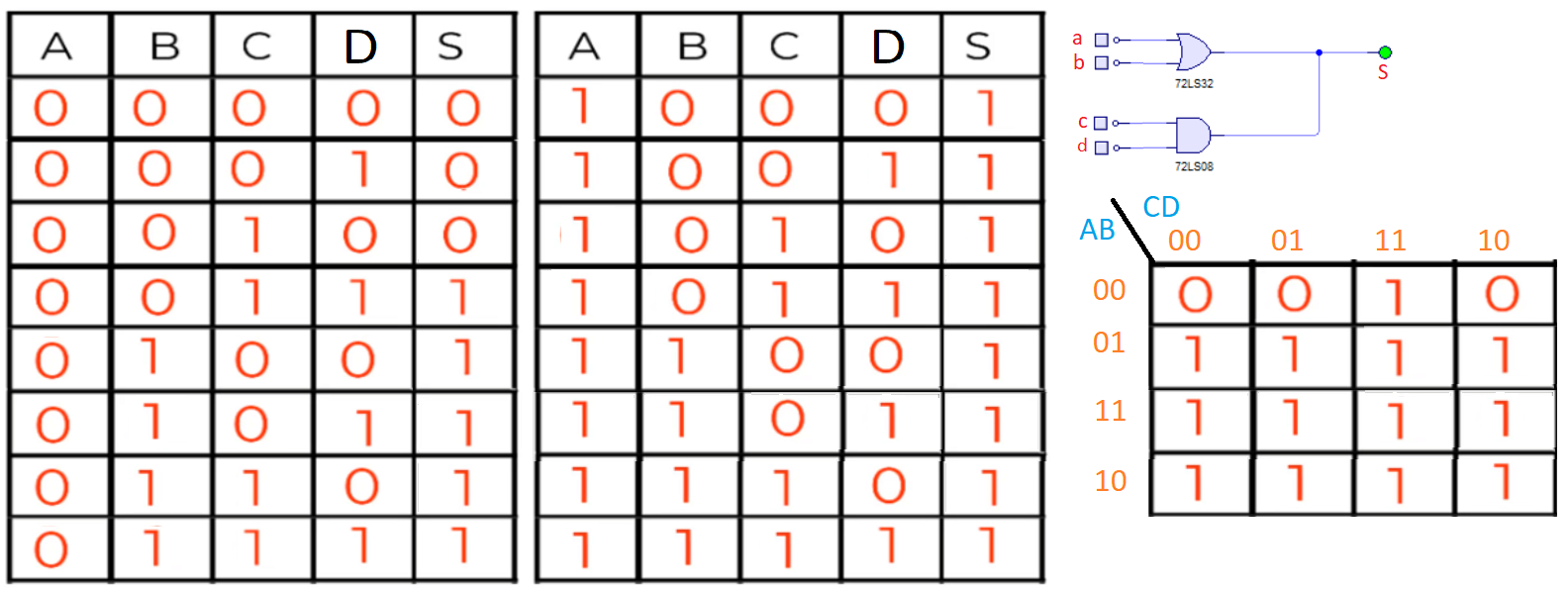
Los mapas se contruyen en una estructura tubular de filas y columnas o columnas y filas. Para construir nuestro mapa de Karnaugh a raíz de un circuito, veamos el siguiente circuito.

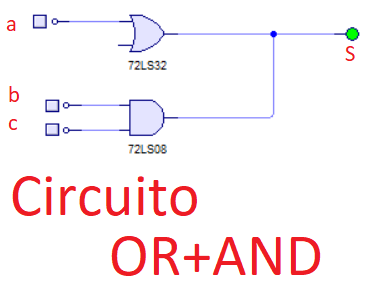
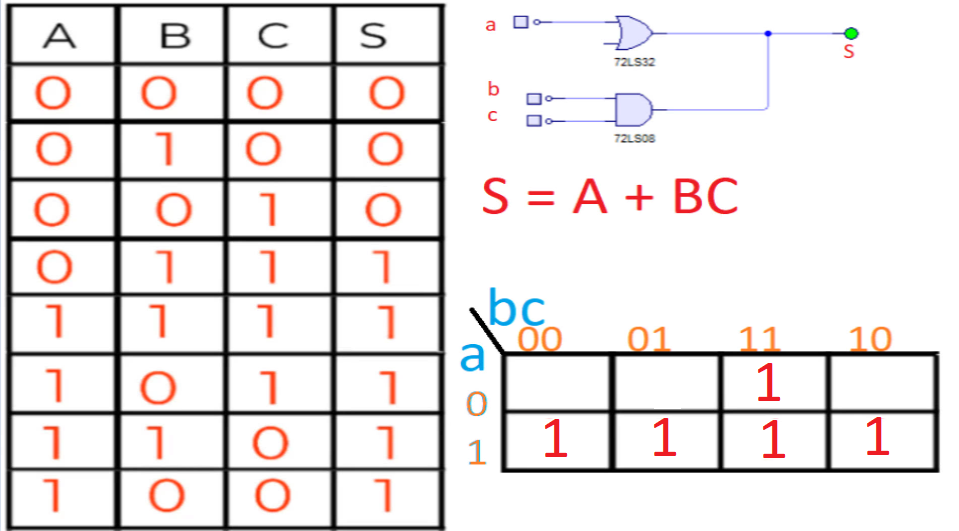
El circuito que puedes ver es el mismo circuito que estamos realizando en la parte teórica de esta clase, en donde tenemos una puerta OR 74LS32 en paralelo con una puerta AND 74LS08, ambas de tecnología TTL. Como puedes ver la salida de las puertas OR y AND se aplican a la salida S. Mientras que sobre A no se aplique tensión, la salida será 0. Si en la puerta AND, no se activan sus dos entradas, tampoco habra salida y el estado será 0. Cuando sobre A se aplica tensión, la salida será 1, independientemente de como estén las variables del AND.

De aquí que podamos sacar la tabla de verdad para el estado de las variables:

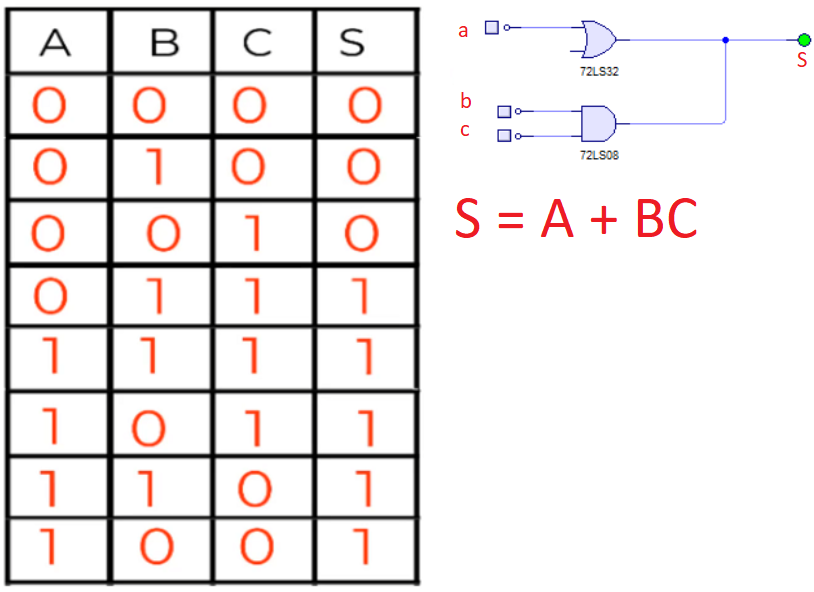
Y a partir de aquí, podemos establecer las ecuaciones maxterms y minterms. Pero vamos a usar Karnaugh para simplificar estas entradas, ya que se cumplen las dos reglas fundamentales para la reducción: que no existan más de 4 variables, ya que son 3; y que necesitemos que reducir las expresiones canónicas maxterms y minterms de la tabla de verdad.

Construcción del mapa.

Una vez definidas las variables vamos a establecer el edificio en donde se van a poner las variables. Hay que tener en cuenta que cuando se traten de 2, 3 ó 4 variables, la estructura de la tupla será diferente. En este caso son tres variables la que entra en el circuito (A, B, C), por lo que, por defecto voy a coger la estructura de filas por columnas que implica en las filas se ponen los valores que pueden coger cada variable independientemente, es decir 0 ó 1. Mientras que en las columnas, se ponen los numerales que cogerán un grupo de variables según puedes ver en la imagen siguiente.

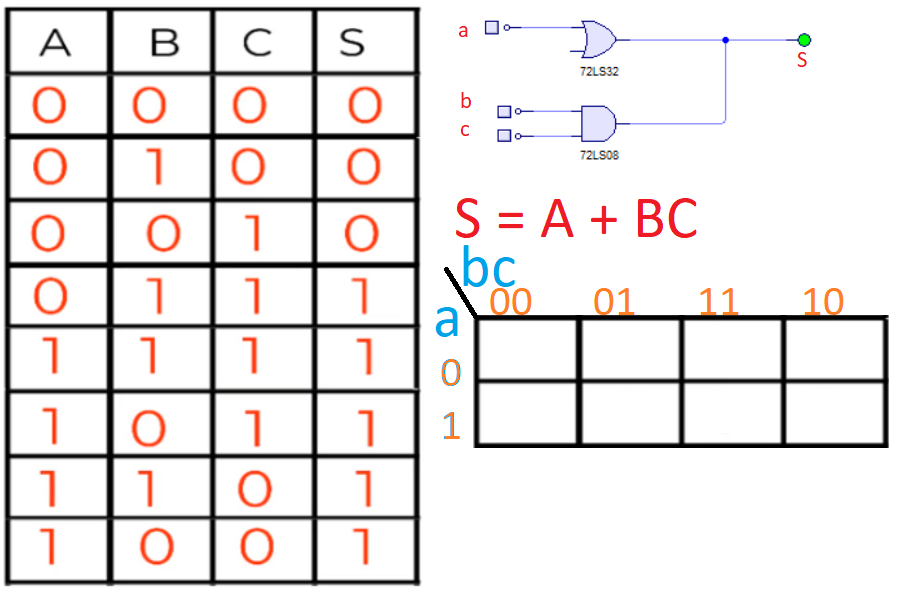
Puedes ver que la estructura al ser de tres variables es la siguiente. Imaginate un mapa en tres dimensiones con la primera variable en la zona de la izquierda del separador superior. Esa variable tiene los valores de 0 y 1, porque solo puede tener dichos valores. En la zona de la derecha del separador, se ponen las otras dos variables con los valores que pueden coger dicho conjunto de variables, es decir el 00, 01, 11, 10. El orden de estas variables es muy importante, ya que siempre cuando pintes el mapa de 3 variables debe de tener esta configuración anterior.

Y ahora, simplemente teniendo la tabla de verdad, vas rellenando según maxterms (por ejemplo), porque solo hay tres 0 en la salida de la tabla de verdad. Y rellenamos de acuerdo a eso:

●Cuando A es 0 (fila), y BC (columna) son 0:

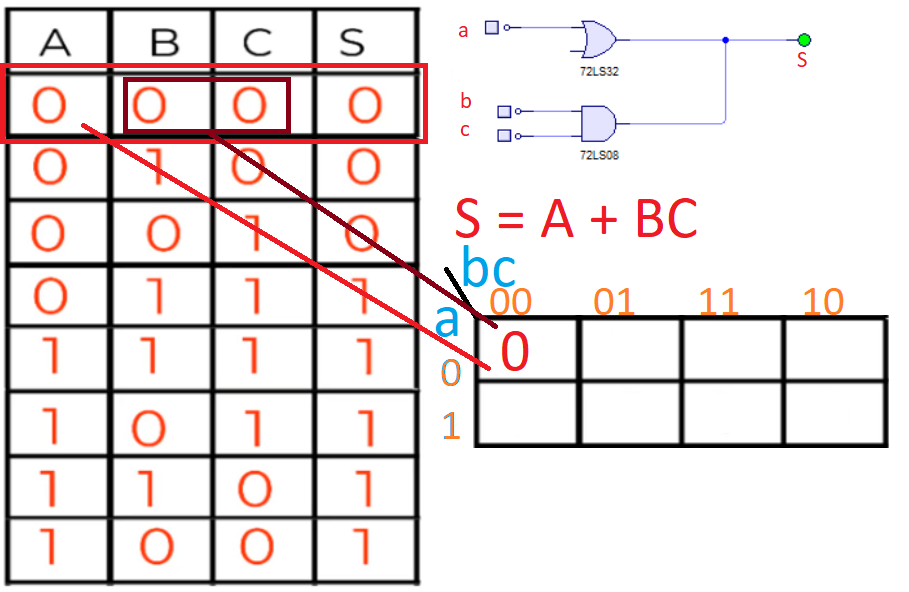
Se pone un cero en dicha casilla que coinciden todas la variables porque la salida es 0. Para la siguiente fila de la tabla de verdad:

● Cuando A vale 0 y BC valen 10:

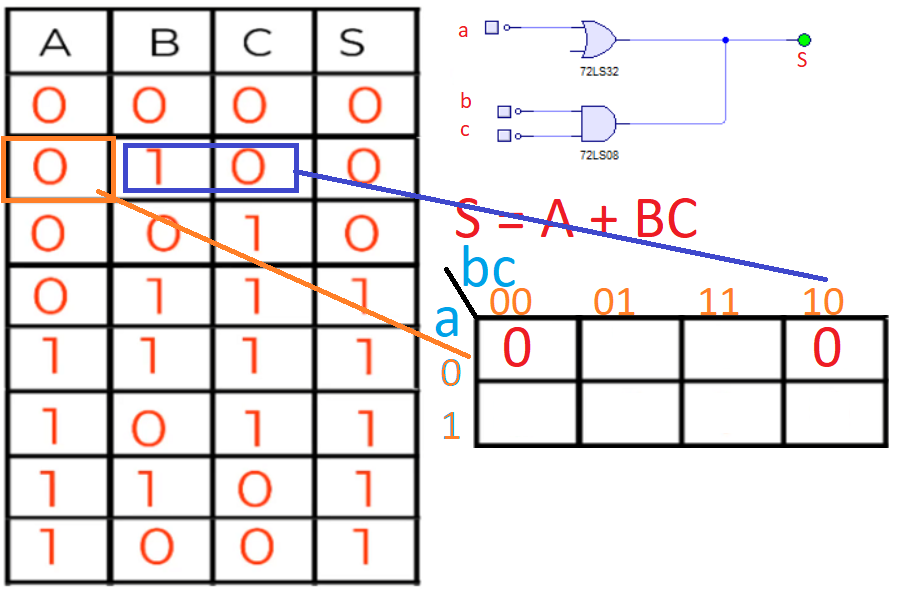
Para la última expresión:

● Cuando A es 0 y BC es 01:

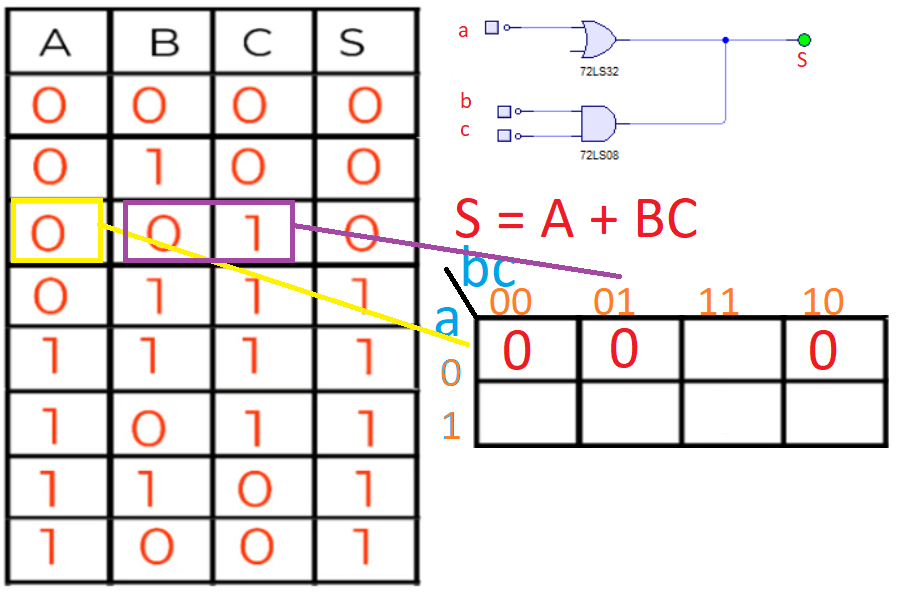
Y ya tenemos todos los ceros de la expresión canónica maxterms. Como lo único que nos quedan son los minterms en el mapa, podemos poner en los espacios vacíos todos los 1 que nos quedan de los minterms, como ves a continuación.

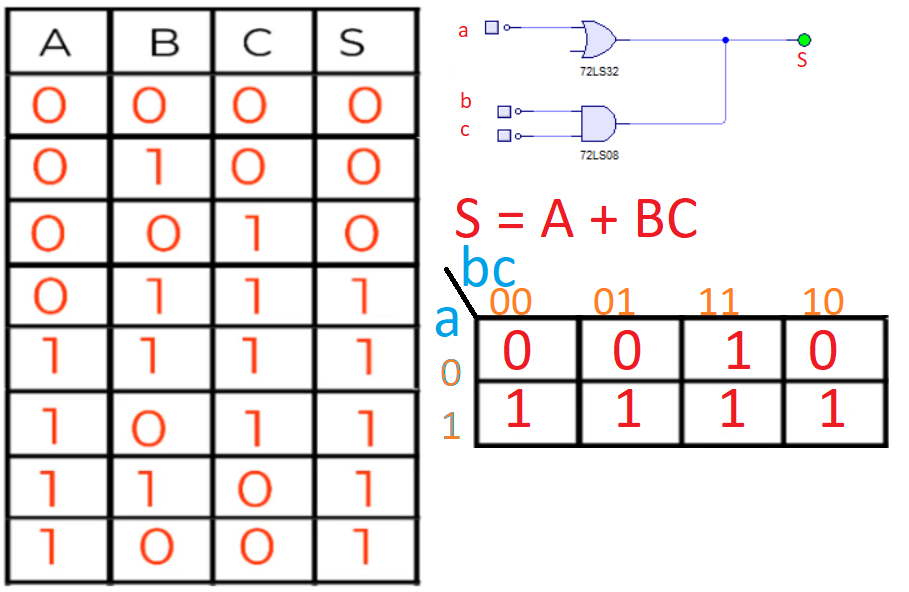
Si utilizaras dos variables tendrías una estructura de dos filas y dos columnas. En las filas estarían los valores posibles de las dos variables, es decir 0, 1; y en las columnas estaría también los dos estados como ves a continuación:

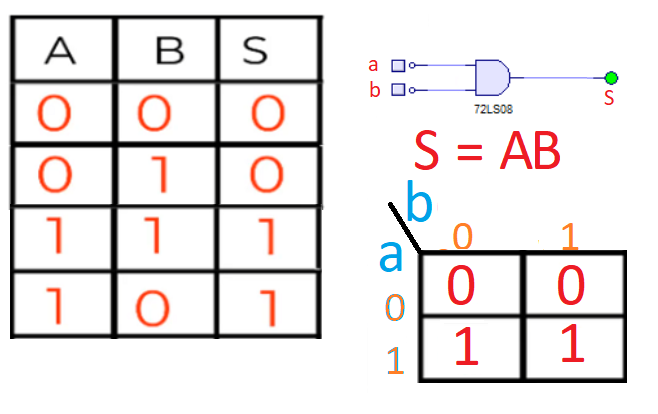
Y cuando tenemos 4 variables, las dos primeras estarán a la izquierda del separador, y las dos últimas a la derecha del separador. Además tanto los números de las filas como de las columnas son los mismos que cuando pintabamos el mapa de Karnaugh para tres variables, pero la tabla de verdad ya tiene 16 registros:

Agrupando variables.

Una vez representado los valores dentro de los mapas de Karnaugh, es hora de agrupar los 1 de acuerdo a una regla específica de unión que se definieron para los mapas de Karnaugh. Y hay que tener en cuenta las casillas adyacentes de la tabla del mapa específico. Vamos a empezar por el mapa de tres variables. Solo vamos a tener en cuenta los 1 del mapa, por lo que si quitamos los ceros quedará así:

Y ahora hay que agrupar los 1 según las siguientes reglas:

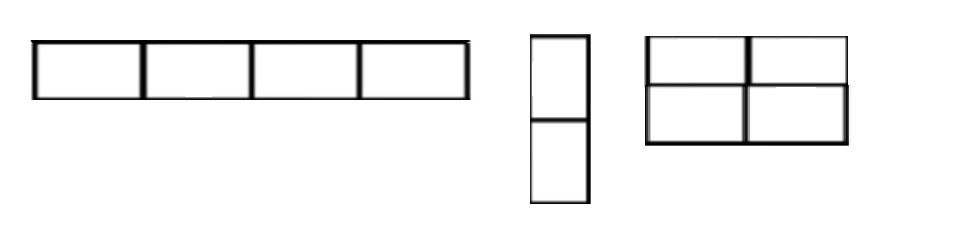
● Se pueden agrupar en grupos binarios de 2, 4, 8 hasta 16 grupos de 1.
● Nunca se agruparán en diagonal.
● Los 1 colindantes también se pueden agrupar ya que el mapa es un mapa tridimensional.
● Evitar la redundancia al seleccionar un 1 que esté seleccionado en otro grupo.
● No se agruparán en números impares, solo pares.

Los 1, se pueden agrupar siguiendo la siguiente plantilla, siempre en números pares:

Vamos a hacer un ejemplo con el anterior mapa de Karnaugh. Vemos que hay cinco 1, y podemos agrupar los 1 de la forma que puedes ver a continuación, agrupando los cuatro de abajo y otros dos en la tercera columna.

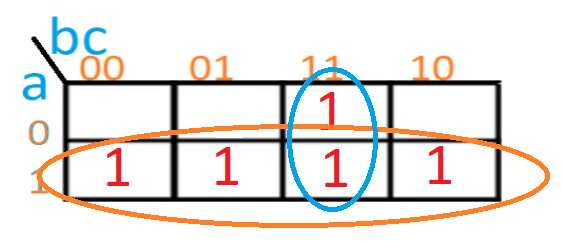
Esta forma de agrupar es lo que se llama "inflar globos" ya que mientras existan 1 y se agrupen de manera par, puede extenderse todo lo necesario. A continuación te muestro alguno otros ejemplos:

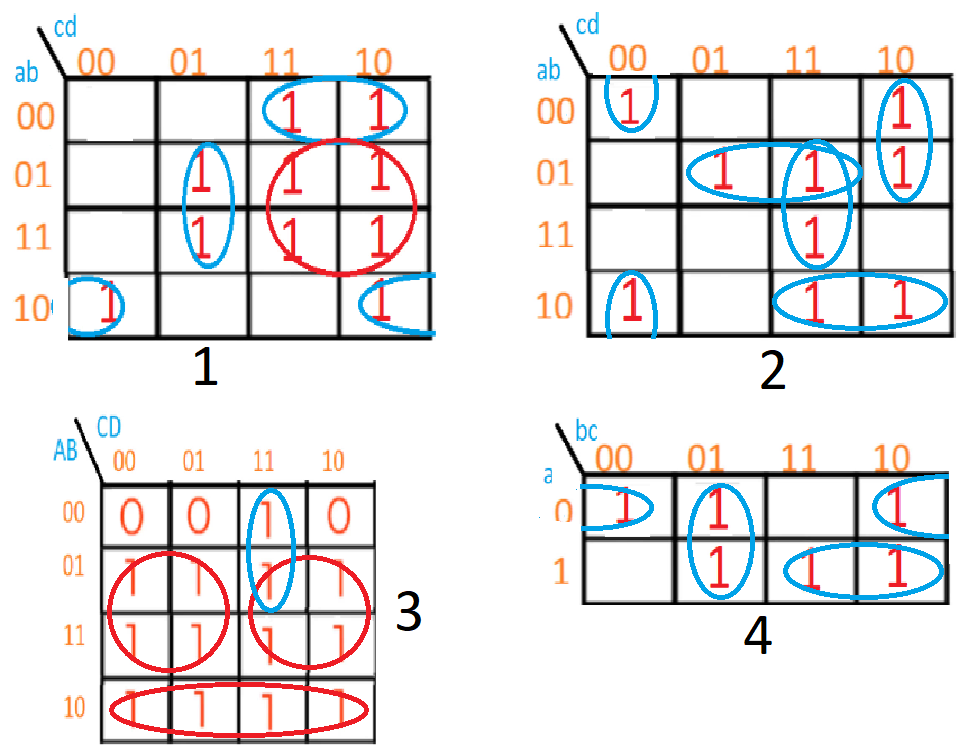
Para sacar las ecuaciones es tan fácil como fijarse en las cordenadas de los ejes X e Y. Por ejemplo en el primer mapa de Karnaugh, el número 1, en la primera fila tenemos los 1 que están estan en las variables cd. Esto según un sistema de coordenadas se puede traducir en:

Variables AB | Variables CD
    ABCD        ABCD     
    0011       0010     

Siendo 0011 el primer número 1 y 0010 el segundo 1 del globo Karnaugh.

Y cómo las cordenadas de AB son 00 para el 1 de la izquierda, y 11 para el mismo 1 de las cordenadas CD, podemos establecer el primer argumento. Para el segundo 1 las cordenadas AB siguen siendo las mismas, pero las cordeandas de CD cambian a 10.

Para sacar las ecuaciones de éste conjunto de 1 anterior, tenemos que tener en cuenta los valores lógicos que coincidan en ambos 1. Por ejemplo:

Variables AB | Variables CD
    ABCD        ABCD     
    0011       0010     

Como puedes ver coinciden las variables ABC con los número 001. Mientras que la variable D no coincide ya que en el 1 de la izquierda es un 1 mientras que en el 1 de la derecha es un 0.

Y la clave está en que solo se tendrán en cuenta los valores que coincidan en ambos unos. Si el valor que coincide es bajo o 0, la variable estará negada; mientras que si el valor que coincide es alto o 1, la variable será normal. Así para la agrupación 0011 - 0010 llamamos a las variables que coincidan, es decir la variable A (0), la variable B (0) y la variable C (1). D no coinciden. Ahora como A y B son ceros, estas variables estarán negadas, quedando este conjunto de la forma:

m0 = ABC

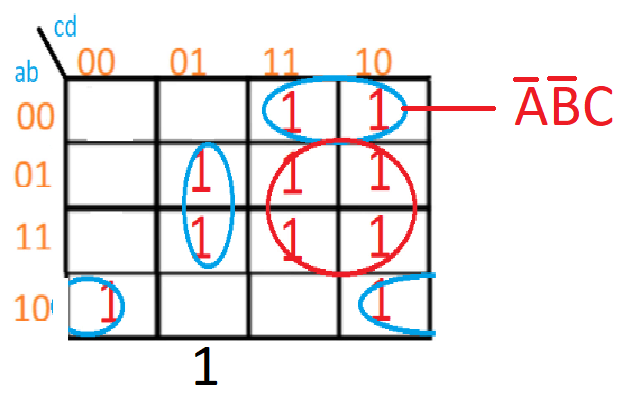
Para el siguiente término, hay que coger las cordenadas de los 4 unos que hay en el globo e ir apuntando los valores uno a uno como ves en la imagen:

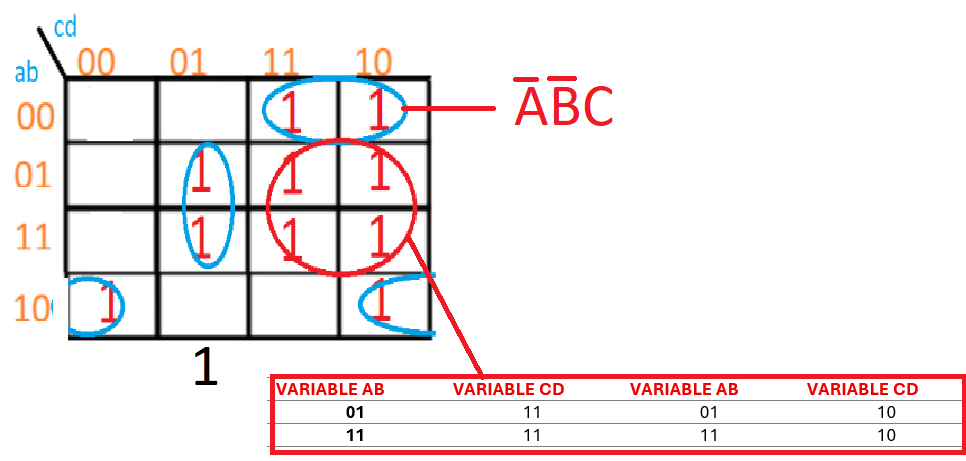
Nos queda que:

ABCD | ABCD | ABCD | ABCD
0110   0111   1111   1110

Siendo comunes solo las variables BC de forma normal, por lo que este conjunto queda como:

m1 = BC

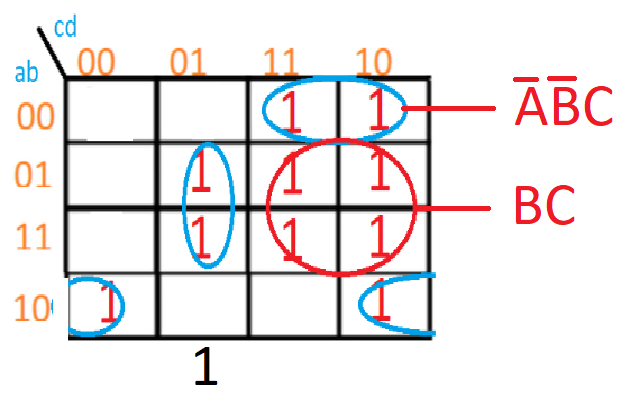
Para el tercer conjunto de globos, quedaría de la forma que puedes ver en pantalla ya que coinciden las variables BCD.

ABCD | ABCD
0101   1101   

Como la variable C es cero en ambos variables, por lo que quedaría este conjunto como:

m2 = BCD

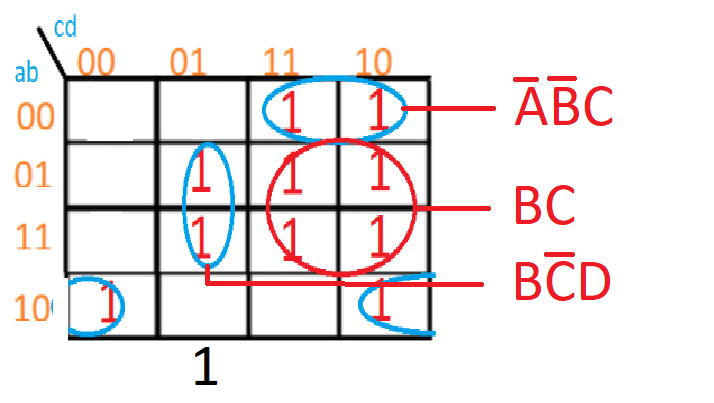
Para el último subconjunto, el que tiene en cuenta los anexos, podemos ver que las cordenadas de ambos unos es 1000-1010, por lo que coinciden las variables A de manera normal, y las variables B y D de forma negada.

m3 = ABD

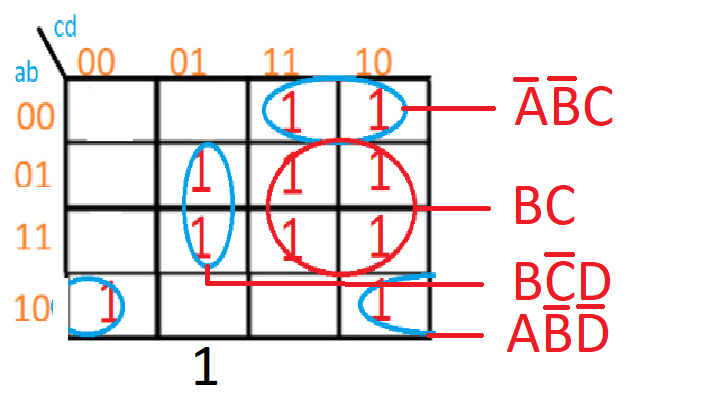
Por lo tanto, en este mapa de Karnaugh obtenemos las ecuaciones mimterms siguientes:

S = m0 + m1 + m2 + m3 = (ABC) + (BC) + (BCD) + (ABD)

Puede resultar un tanto lioso este método de reducción de ecuaciones, pero verás como según vayas practicando, podrás sacar las ecuaciones de una manera más fluida.

Gracias por compartir y ayudar a que mi proyecto siga creciendo y ganando subcriptores. Te lo agradezco.