ALGEBRA DE BOOLE.

En la clase teórica hemos adelantado los conceptos para entender la electrónica digital. En esta clase vamos a seguir ampliando conceptos.

La electrónica digital se compone fundamentalmente de puertas lógicas, que basicamente son las que realizan las funciones lógicas. Cuando hablamos de una función AND, lo que estoy indicando es que la puerta lógica AND es un componente eléctrico específico para realizar esa función. También hay puertas lógicas para la función OR, la XOR, la NOT, etc., etc. Aunque muchas de ellas ya tienen integradas varias de estas funciones con estructura interna.

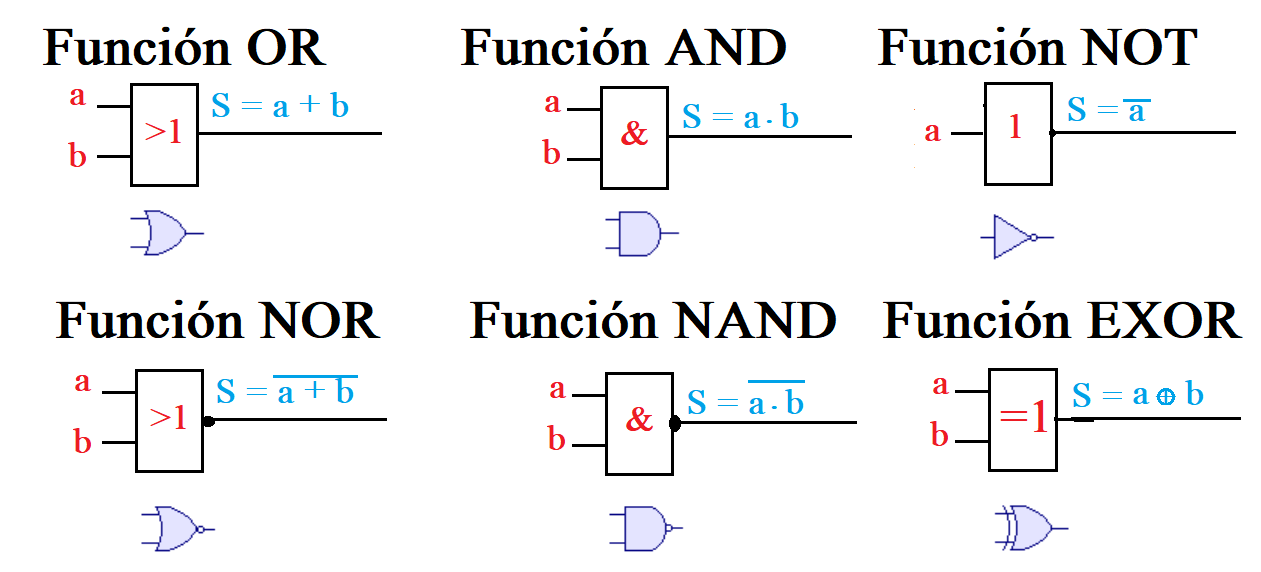
La tecnología que es usada hoy en día en las puertas lógicas es una familia TTL y CMOS, que son las más extendidas. La familia TTL es la familia lógica de las tecnologías bipolares y han sido muy usadas en el pasado. Pero hoy en día ha ganado las familias de CMOS, que son están integrados dentro de la tecnología unipolar.

En la mayoría del curso veremos tecnología TTL pues la tecnología mejor implantada dado su larga duración. Pero no descarto mirar otras tecnologías más modernas.

Estos circuitos que veremos nos ayudarán a entender cómo funciona el álgebra de Boole.

Principio de dualidad.

Leyes de Boole.

El principio de dualidad es aquel que dice que, si tenemos una expresión lógica y cambiamos la función lógica y se complementan los 0 ó 1 que aparezcan (invierten), obtendremos otra expresión lógica correcta.

Este método te permitirá obtener unas funciones lógicas partiendo de otras.

En el álgebra de Boole existen también propiedades derivadas de las funciones lógicas.

Propiedad conmutativa.

Propiedad asociativa.

Propiedad distribuitiva.

Ley de absorción.

Teorema de Shannon.

Teorema de De Morgan.

Expresiones canónicas de una función.

En este tipo de términos, porductos, también se denominan minterms, y por ello también se dice expresión en minterms.

Este tipo de términos, suma, también se llaman maxterms y por ello estas formas canónicas se conocen como expresión en maxterms.

Obtención de la tabla de verdad canónica.

Expresiones canónicas de una función.

Ejercicios resueltos.

En esta parte de la teoría vamos a resolver algunos ejercicios para que entiendas perfectamente estos conceptos quehemos visto hasta ahora.

Demostrar las siguientes propiedad del álgebra de Boole por medio de tablas de verdad y de forma algebraica.

A + (BC) = (A+B)(A+C)

Esta es una propiedad distribuitiva de la suma respecto al producto, que sólo es correcta en el álgebra de Boole.

Existe un equivalencia entre las dos expresiones, además de poder hacerlo algebraicamente y mediante circuitos eléctricos. También podemos sacar la tabla de verdad. Para ello hay que hacer cada operación que aparece en la expresión algebraica y combinarlas finalmente:

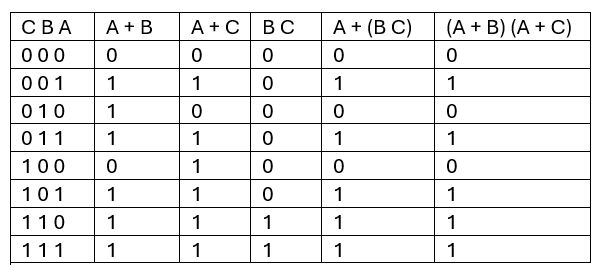
Se puede demostrar algebraicamente separando términos:

Dibujar los circuitos que corresponden a las siguientes expresiones.

S1 = ĀB + C D

En este circuito las expresiones que aparecen son negadas teniendo en cuenta que la suma lógica la realiza la puerta O, la operación producto, la puerta Y, y las complementarias las realiza el inversor.

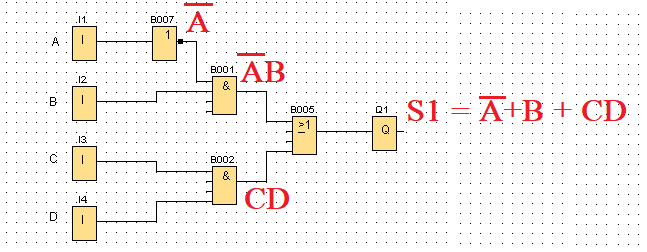
S2 = A + B + CD

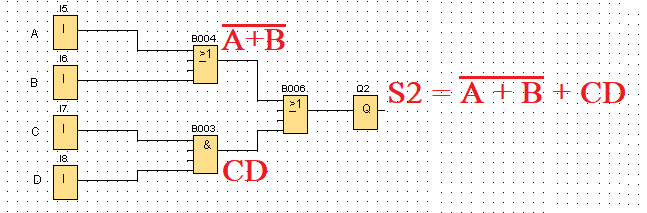
Resumen.

Para diseñar un circuito digital combinacional es conveniente comenzar por elaborar la tabla de verdad, donde se indicarán todas las posibles combinaciones de entrada y qué valor adoptará a la salida. A partir de la tabla se obtienen las ecuaciones del circuito.

Estas ecuaciones se pueden obtener en forma de suma de productos o Minterm, o en forma de productos de suma o Maxterm.

Minterm.

Cada una de estas combinaciones originará un Minterm en el que aparecerán las variables de entrada relacionadas mediante productos lógicos. Si la variable binaria toma el valor de 1, en dicha combinación aparecerá de forma directa; si toma el valor 0, aparecerá de forma negada.

Maxterm.

Cada una de estas combinaciones originará un Maxterm en el que aparecerán las variables de entrada relacionadas mediante sumas lógicas. Si la variable binaria toma el valor de 0, en dicha combinación aparecerá de forma directa; si toma el valor 1, aparecerá de forma negada, todo lo contrario a lo que ocurre con los Minterm.

Cuadro de comprobación.

La regla fundamental es que para n variables de entrada se disponen dos combinaciones por su estado binario.

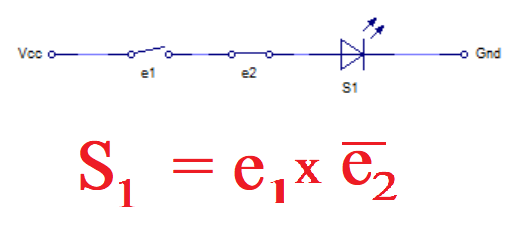
Por ejemplo, para una variable binaria, tenemos 2¹ = 2 combinaciones. Para 2² tenemos 4 combinaciones, como en el caso anterior. Si aumentamos las variables del circuito, aumentamos el valor de las combinaciones, por lo tanto se aumenta la ecuación de la función del circuito lógico.

En el circuito anterior, obtenemos 4 combinaciones con las dos variables binarias de entrada. La variable e₁ y e₂ nos producen las siguientes salidas:

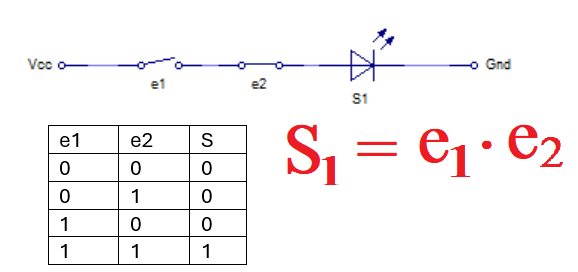
A partir de este cuadro se puede deducir la ecuación S₁. Este resultado es la suma de los términos para los que S₁ = 1.

Aquí unicamente vale que e₁ = 1, y e₂ = 1, es decir S = e1e2.

Volvemos a tomar la ecuación del siguiente circuito:

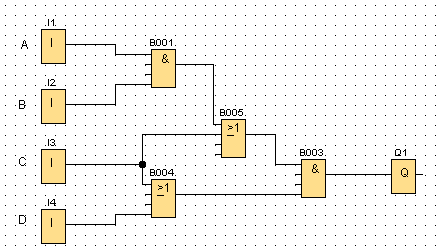
A primera vista puede parecer un poco complicado, pero lo primero que tienes que hacer es crear la tabla de verdad para cada entrada binaria. Si tenemos 4 entradas, sabemos que van a existir 2⁴ combinaciones. Pues ya sabemos que son 16 entradas.

NOTA: Para pintar la tabla de la verdad, según el número de variables, empezamos a agrupar los grupos de bits de izquierda a derecha. Así por ejemplo, la variable más a la izquierda tendra en este caso los 2 bytes de información pintados (8 ceros y 8 unos). La segunda variables a la derecha, tendrá 1 byte mixto (4 ceros y 4 unos); el siguiente a la derecha tendrá 4 bits, repartidos entre dos ceros y dos unos repetitivos. La última variable tendrá un 0 y un 1 y repetirá continuamente el valor.

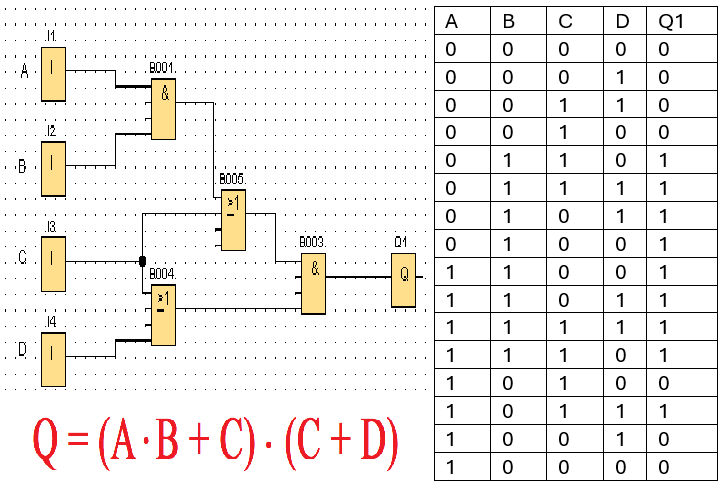
Fijate que esta configuración que se usa a la hora de pintar los estados en cada variable, es una progresión que refleja el codigo GRAY, como vimos en la clase anterior.

Gracias por compartir y ayudar a que mi proyecto siga creciendo y ganando subcriptores. Te lo agradezco.